Week 1. Dynamic Connectivity 动态连通性

  1. 将所有对象映射为0-N
    证明：一棵树上的节点x的深度最多为lgN
    两棵树大小相等时，union操作会使合并得来的新树大小翻倍，但是高度只+1
    （也可以理解为每次树的高度+1，树的大小则翻倍）
    因此假设树最开始只有一个节点，经过lgN次翻倍后形成完整的节点数为N的树，此时树的高度为lgN!
Reference

Exercises Solution

3-sum算法

upper bound为O(N^2logN) （二分查找logN * N^2）
lower bound至少为Ω(N) （有可能更高，但目前没有证明）因为算法至少需要遍历一遍所有数字，否则可能会漏过

证明一个算法是最优的（或者优化一个算法），要不降低算法的upper bound，要不证明算法有更高的lower bound
（即缩短上下bound之间的gap）
当upper bound = lower bound即证明算法没有其他更优解

Big O记号常常用来表示一个算法的性能，但这是错误的，他只表示一个算法的上界。比如：函数$2n^2$，$25000n^3$都可以用$O(n^3)$表示。改用tilde标记 ~$2n^2$来表示特定算法的性能

内存使用

Types Bytes Types Bytes
char 2 char[] 2N + 24 (Overhead)
int 4 int[] 4N + 24 (Overhead)
double 8 double[] 8N + 24 (Overhead)
boolean 1 char[][] ~ 2NM
float 4 int[][] ~ 4NM
long 8 double[][] ~ 8NM

Java对象 Obejct：
Object Overhead: 16 Bytes
Padding: 填充字节，使得整个object的大小为8的倍数
Object的大小= 16 (Overhead) + 变量大小 + Padding
e.g. 下面类产生的object有32个字节：16(overhead) + 4*3(variables) + 4(padding)

1
2
3
4
5
public class Date {
    private int day;
    private int month;
    private int year;
}

指针大小 (reference)：8 Bytes (64位) / 4 Bytes (32位)

Week 2. Stack & Queue 堆栈和队列

resizing array

如果每添加一个数字，将array扩大1位，则插入N个数据的数组的访问次数为1 + 2 + … + N ~ 0.5 N^2

Loitering问题

将数组某项设为null，如A[0] == null，可以释放相应的空间 （Stack的array实现中，push操作后需要把相应位置设为null）

Optimal Soultion:

初始设array大小为1，每次array将满的时候，将array扩大一遍
此时array的访问次数大概为 N + (1 + 2 + 4 + 8 + … + N) = ~3N
当数组只有1/4满的时候，才将数组大小减半 （防止thrashing抖动问题）

Performance

push 和 pop 操作最好情况下性能为O(1)
由于resizing操作，最坏情况（worst case）下性能为O(N)
（对比linkedlist实现，最好最坏情况均为O(1)）

Memory Usage

对stack的Linkedlist实现，需要空间为 40N Bytes （一个节点40 Bytes）
对array实现，当数组全满时，空间为8N，当数组为1/4满时，空间为32N

LinkedList vs Resizing Array

链表实现，每个操作都是常数操作，但需要额外空间和用于分配空间的时间，因此平均性能较慢，但比较稳定
数组实现，所需空间和运行总时间较少，但可能某个操作遇到需要resize的情况导致效率变慢，性能较不稳定

Java Generics (Java泛型)

之前设计的都是String类型的stack和queue，如果我们想要实现任何数据类型都可以接收的stack和queue，就需要用到java泛型

Example：创建一个泛型的stack类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class stack<Item> {
//这里预先定义一个Item的数据类型，以后使用的时候可以替换为其他数据类型
    private class Node {
        Item item; //这里引用Item，表示任意传入的数据类型
        Node next;
    }
    
    public Item pop() {
        ...
    }
    
    ... //其他函数或变量
    
}

如果要使用这个类的对象，可以使用
Stack<Integer> integerStack = new Stack<Integer>();命令创建一个接受Integer的stack对象

注意：Java不能创建泛型数组
如果需要将上面的stack改为数组实现，则可以创建一个Object数组，再将其cast强制转换为Item[]类型的数组：
Item[] S = (Item[]) new Object[capacity];

另外，Java泛型只接受包装数据类型（Wrapper Type），如Integer，String，Double，基本类型（Primitive Type，如int, double）需要转换为包装类型才能用于泛型
在一些高版本的java支持Autoboxing(自动打包)，可以直接传入基本数据类型

Iterator 迭代器

Java提供了一种Iterator迭代器机制，可以帮助我们遍历一个class中的所有元素（比如说遍历stack和queue中的元素）

步骤（以stack为例）：

  1. 创建一个stack类，并实现（implement）iterable接口
1
2
3
public class Stack <Item> implements Iterable<Item> {
    
}

这里，Iterable<Item>里面的Item是你要迭代(遍历)的元素的数据类型

  1. 要实现这个Iterable接口，代表这个stack类中需要有一个iterator函数，这个函数返回一个类型为Iterator<Item>的实例
    (即返回一个迭代器实例，这样Java每次调用迭代机制的时候会调用这个iterator()函数生成一个新的迭代器)
1
2
3
public Iterator<Item> iterator() {
    return new ListIterator();
}
  1. 用一个内部类来实现(implement)我们的迭代器
1
2
3
4
5
6
7
8
9
private class ListIterator implements Iterator<Item> {
    public boolean hasNext() {
        ... //确定是否能继续迭代
    }
    
    public Item next() {
        ... //返回下一个元素
    }
}

注意这里Iterator<Item>是已经预置在Java里面的内部类（其实是一种较为特殊的类称为Interface 接口），类似于一个迭代器模板，我们需要的是创建一个新的迭代器类，但是要按照这个迭代器模板实现（所以是implements Iterator<Item>）
因为Iterator这个类名已被占用，所以我们创建的新的迭代器类不能命名为Iterator（这里命名的为ListIterator）

Example
假设我们有一个stack对象Stack<String> ourNewStack = new Stack<String>()，并且这个stack类实现了iterator
当我们执行语句 for (String item : ourNewStack)时：

  1. Java首先调用这个类中的iterator()函数来创建一个新的Iterator实例，这个实例里面包含hasNext() 和 next()两个methods
  2. Java首先调用hasNext()来判断是否有下一个元素，再调用next()来返回下一个元素，直到所有元素遍历完成
Bag 包

利用迭代器可以实现一种名为Bag的数据结构，可以将item放入bag，然后遍历所有放入bag中的item

Week 3. Sort Algorithm 排序算法

Ref: Comparable接口

假设我们新定义了一个日期数据类型Date，里面包括三个int变量month, day, year
对于任意两个Date变量，我们想要他们可以比较大小，就需要对这个Date的class实现Compareable接口，包括一个compareTo函数来定义如何比较大小

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Date implements Comparable<Date> {
    private final int month, day, year;
    public Date (int m, int d, int y) {
        month = m; day = d; year = y;
    }
    
    public int compareTo (Date anotherDay) {
        //如果this Date > anotherDay; return 1;
        //如果this Date < anotherDay; return -1;
        //如果this Date = anotherDay; return 0;
        //需要具体实现以上比较规则
    }
}

我们可以利用Comparable类定义两个通用的helper function，在将来的排序算法中能够简化代码量：

  1. less (用于判断变量v是否小于变量w)
1
2
3
private static boolean less(Comparable v, Comparable w) { 
    return v.compareTo(w) < 0;
}
  1. Exchange (假设有一个已经实现了comparable接口的数据类型的数组a，交换数组第i项和第j项的数据)
1
2
3
4
5
6
private static void exch(Comparable[] a, int i, int j)
{
   Comparable tmp = a[i];
   a[i] = a[j];
   a[j] = tmp;
}

Note: 这里的Comparable接口和前面的Iteratable接口、Iterator接口类似，都用到了java泛型，本质上都是一个模板类，里面有一些预先定义的函数（iterator(); compareTo(); hasNext(); next();），java系统可以根据模板对实现了这些接口的数据类型调用这些函数

Selection Sort 选择排序

设立一个数组的指针i从左向右移动
每移动一位，遍历指针i右侧(包括i)的所有项，选择(select)其中最小的项，与当前指针i所指的项交换
这样能保证指针左侧的数据已经是排好序的，当指针i遍历到最右时所有数据已排好序

代码

1
2
3
4
5
6
7
8
9
public static void selectionSort(Comparable[] a) {
    for (int i = 0; i < a.length; i++) { //移动指针
        int min = i;
        for (int j = i+1; j < N; j++)
            if (less(a[j], a[min]))
                min = j; //找出指针i右侧最小的项
        exch(a, i, min); //交换最小项至当前位置
    }
}
Complexity

最好和最坏情况下都需要(N-1) + (N-2) + … + 1 + 0 = N^2/2次比较大小操作和N次交换操作
时间复杂度为O(N^2)，空间复杂度为O(N)

Insertion Sort 插入排序

同样设立一个数组的指针i从左向右移动
对于i指向的数据，如果他小于他左边的项，则和左边的数据交换
交换之后如果还小于左边的数据则继续交换，直到不小于为止（即指针i左侧的数据全部排好序）

1
2
3
4
5
6
7
8
public static void insertionSort(Comparable[] a) {
    int N = a.length;
    for (int i = 0; i < N; i++) //移动指针
        for (int j = i; j > 0; j--) //从当前位置开始往左交换
            if (less(a[j], a[j-1]))
                exch(a, j, j-1);
            else break;
}
Complexity

最好情况下，数组本身已排好序，因此需要N次比较和0次交换
最坏情况下，数组为倒序，需要N^2/2 次比较和N^2/2次交换（比Selection Sort慢）
对于一个已经部分排好序（partially sorted）的数组，Insertion sort所需时间是线性的
对于随机的数组，平均需要N^2/4 次比较和N^2/4次交换
时间复杂度为O(N^2)，空间复杂度为O(N)

Shell Sort 希尔排序

1. h-sort

本质上是Insertion sort，只是每次比较和交换时，和往左数第h个数进行比较和交换
（h为1时即为Insertion sort）

2. Shell sort

设定一个较大的h（h < a.length），进行h-sort
缩小h再进行h-sort，直到h为1
经过多次h-sort使得数组部分排序，这样最后进行insertion sort所需比较和交换次数会大大降低

如何确定h序列？
一般采用3x+1，即1, 4, 13, 40, 121, 364, …

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static void sort(Comparable[] a) {
    //确定最大的h
    int h = 1
    while (h < N/3) h = 3*h + 1;
    
    while (h >= 1) {
        // h-sort
        for (int i = h; i < N; i++) { //指针（从h开始，因为h往左的项没办法和再左边的第h项比较）
            //比较和交换往左数第h项
            for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) 
                exch(a, j, j-h);
        }
        h /= 3; //缩小h，在进行h-sort，直到h为1 (Insertion sort)
    }
}
Complexity

Worst case: $O(N^{3/2})$
Average: O(NlogN) ~$N^{1.289}$

Ref Application1：Knuth Shuffle 洗牌算法

设立一个指针i，从左往右移动
每移动一位，生成一个[0,i]之间的随机数r，交换第i位和第r位 

1
StdRandom.uniform(i + 1); //生成[0, i+1)的随机数

Ref Application2: Convex Hull 闭包算法

问题描述：平面中有一堆点，找出最少的点，这些点连起来围成一个圈可以包括所有点
观察：闭包上的点，总可以通过逆时针旋转得到下一个点
算法:

  1. 找出一个原点p，这个点具有最小的y-coordinate
  2. 将原点p和其他点连线，连线与y轴的夹角称为polar angle，按照polar angle从小到大的顺序依次遍历除p外所有点
  3. 将第一个点放入堆栈s
  4. 如果遍历到的点和堆栈s中的顶点组成了一个逆时针旋转(ccw turn)，则将该点入栈，否则将顶点出栈再将该点入栈
  5. 最后留在栈s中的点则为闭包上的点

如何判断三个点是否呈逆时针旋转 

1
2
3
4
5
6
public static int ccw(Point2D a, Point2D b, Point2D c) {
    double area2 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
    if (area2 < 0) return -1; // clockwise
    else if (area2 > 0) return +1; // counter-clockwise
    else return 0; // collinear
}

Merge Sort 归并排序

分治法的应用，将一个大数组分成两个小数组，分别排好序，再合并为一个排好序的大数组

  1. Merge函数
    假设一个数组，左半部分和又半部分已经单独排好序，现在需要排序整个数组
    需要一个aux辅助数组复制a数组，lo和hi指针分别指向两个子数组的头元素，mid为第一个数组的尾元素
    依次复制lo和hi指针指向的aux中的元素的最小值回a数组，并相应更改lo和hi指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi){
    //前置条件
    assert isSorted(a, lo, mid); // precondition: a[lo..mid] sorted 
    assert isSorted(a, mid+1, hi); // precondition: a[mid+1..hi] sorted 
    
    //复制数组
    for (int k = lo; k <= hi; k++) aux[k] = a[k];

    //归并数组
    int i = lo, j = mid+1;
    for (int k = lo; k <= hi; k++) {
        if      (i > mid)              a[k] = aux[j++];
        else if (j > hi)               a[k] = aux[i++];
        else if (less(aux[j], aux[i])) a[k] = aux[j++];
        else                           a[k] = aux[i++];
    }
    //检查数组是否排好序   
    assert isSorted(a, lo, hi); // postcondition: a[lo..hi] sorted 
}
补充：Java Assertion 断言机制

用于debug和提示代码功能
e.g. 假设函数isSorted(a, lo, hi)用来判断数组a从第lo位到第hi位的元素是否排好序，在merge sort中我们需要merge两个排好序的数组，这样我们就可以在merge前加入assert isSorted(a, lo, hi)代码，如果两个子数组没有排好序就可以提前报错，方便debug；也可以在merge后加入，用于检验我们的merge算法是否准确，同时也方便说明这段merge代码的作用
(注意：assertion是默认不启动的，需要在运行时加入java -ea myProgram)

  1. MergeSort
    有了merge函数，现在可以很方便的递归分割数组，再用merge函数合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
    if (hi <= lo) return; //跳出递归条件（只有一个元素的时候）
    int mid = lo + (hi - lo) / 2;
    sort(a, aux, lo, mid);
    sort(a, aux, mid+1, hi);
    //当左数组的最大值小于右数组的最小值，代表整个数组已经排好序，因此不用merge以节省时间
    if (!less(a[mid+1], a[mid])) return;
    merge(a, aux, lo, mid, hi);
}

public static void sort(Comparable[] a) {
    aux = new Comparable[a.length]; //在这里创建aux数组并传入merge以避免重复创建
    sort(a, aux, 0, a.length - 1);
}
Complexity

时间复杂度: ~NlgN (linearithmic)；空间复杂度： ~N （需要额外Aux辅助数组）

证明1：
假设D(N)为对总长度为N的数组的两个子数组进行merge所需要的比较和数组access的数量，则有:
D(N) = 2D(N/2) + N (归并需要N次比较)
往下递归一层，则有: D(N/2) = 2D(N/4) + N/2
需要进行两次D(N/2)，因此这层所有的D(N/2)需要(N/2) * 2 = N次比较
同理再往下一层，有D(N/4) = 2D(N/8) + N/4，需要进行2*2=4次D(N/4)，一共N次比较
因此一直递归到底层D(2)，每层都需要N次比较
由于分治法，一共有lgN层，因此时间复杂度为NlgN

证明2（数学归纳法）：
Base case：D(1) = 1
假设：D(N) = NlgN
证明：D(2N) = 2Nlg2N

因为D(N) = 2D(N/2) + N
所以D(2N) = 2D(N) + 2N
= 2NlgN + 2N
= 2N(lg(2N)-1) + 2N
= 2Nlg2N

改进方法1：CUTOFF

对于一些小数组，或者递归到一定程度数组比较小的时候，可以直接采用insertion sort以避免不必要的递归开销
假设预先设定一个CUTOFF值，当数组总长度小于CUTOFF值时对整个数组采用insertion sort（相当于base case）

1
2
3
4
5
//base case 
if (hi <= lo + CUTOFF - 1) {
    Insertion.sort(a, lo, hi);
    return; 
}

经验证当CUTOFF=7，可使MergeSort提升20%速度

改进方法2：Buttom-up Sort（自下而上的递归）

从左到右，两两元素一组进行merge操作，在4个4个元素一组进行merge，一直增大直到merge元素的长度等于数组的实际长度

1
2
3
4
5
6
7
public static void sort(Comparable[] a) {
    int N = a.length;
    Comparable[] aux = new Comparable[N];
    for (int sz = 1; sz < N; sz *= 2) //每次扩大要合并数组长度为两倍
        for (int lo = 0; lo < N-sz; lo += sz+sz) //遍历，两两一组
            merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
 }

优点：不需要递归，但比递归法慢10%

Quick Sort 快速排序

和merge sort同属递归分治法，但先完成相应的部分排序操作，再往下递归缩小问题规模（和merge sort先递归到底再从下往上进行排序操作相反）

0. 预先操作：shuffle the array

对数组随机洗牌，避免worst case

1
StdRandom.shuffle(a); // 传入Comparable[] a
1. 基本步骤：Partition the array

随机从数组中选取一项v，并将数组分为两部分，使得数组左边所有项小于v，数组右边所有项大于v
（注意：这里当存在duplicate key即存在和v相等的项时，指针跳过该项并继续移动，而非交换）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private static int partition(Comparable[] a, int lo, int hi) {
    int i = lo, j = hi+1; //设立左右两个指针i，j，并以a[lo]为基准进行Partition分区
    while (true) {
        while (less(a[++i], a[lo]))     //找出数组左边大于基准a[lo]的数，准备和右边小于a[lo]的数交换
            if (i == hi) break; //如果左指针i已经移动到数组右端，则停止移动
            
        while (less(a[lo], a[--j])) //找出数组右边小于基准a[lo]的数，准备和左边大于于a[lo]的数交换
            if (j == lo) break; //如果右指针j已经移动到数组左端，则停止移动（redundant：该命令事实无效）
      
        if (i >= j) break; //如果左右两指针交叉，则数组已完成分区
        exch(a, i, j); //交换左右指针所指的数据
    }
    //数组分完区后，由于指针交叉，右指针j会指向左分区最后一个数，左指针i会指向右分区第一个数
    //因此交换右指针j和指针lo所指向的数据，使得基准a[lo]（此时应该在a[j]的位置）的左边所有数
    //小于基准，右边所有数大于基准
    exch(a, lo, j); 
    return j; //这里返回基准的位置（即分区点）
}
2. 递归

分别对左右两分区进行再分区操作，直到分区的大小为1或0

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
//init：对数组进行洗牌（这样分区后的子数组同样也是随机排列）
public static void sort(Comparable[] a) {
    StdRandom.shuffle(a);
    sort(a, 0, a.length - 1);
}

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return; //base case，右指针小于等于左指针
    int j = partition(a, lo, hi); // 先分区
    sort(a, lo, j-1); //对左分区进行排序
    sort(a, j+1, hi); //对右分区进行排序
}
Complexity

Time: ~NlogN (1.39NlogN)
Best case：每次分区点都为中点，同merge sort，每层递归需要N次比较，一共有lgN层，
因此一共需要N*lgN = NlogN
Worst case：每次分区点都为起点，则一共有N层递归，假设为第i层，则需要i次比较，因此复杂度为~0.5 N^2 (very unlikely)
Average: ~1.39NlogN (随机洗牌)

所需compare的次数和Merge sort相比大于39%，但所需交换次数更小，因此速度比merge sort快
但merge sort能保证在worst case下依然有~NlogN的复杂度（因为每次递归一定是对半分）而quick sort不能保证（虽然经过洗牌后worst case基本不可能发生），因此相较之下merge sort更稳定

Space: ~lgN
每层递归都需要常数级别空间（指针等），一共有lgN层
和Merge sort相比可以实现in-space，即不需要额外空间

改进方法1：Cut Off

同merge sort，当递归到一定程度，数组比较小的时候，可以直接用insertion sort (CUTOFF ~ 10)：

1
2
3
4
5
6
7
8
9
private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo + CUTOFF - 1) { //base case
        Insertion.sort(a, lo, hi);
        return;
    }
    int j = partition(a, lo, hi); // 先分区
    sort(a, lo, j-1); //对左分区进行排序
    sort(a, j+1, hi); //对右分区进行排序
}

经验证将CUTOFF设为10到20，能使Quick sort速度平均提升20%

改进方法2：Median of Sample 随机采样基准点

随机抽取数组中3个点（一般取数组左右端点和中点，即lo, hi 和 lo + (hi - lo)/2），
找出其中的中位数并将其设为基准点（即交换到左端点位置），
这样找出的基准点能使两分区大小大致相等

1
2
3
4
5
6
7
8
9
10
private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return;
    
    int m = medianOf3(a, lo, lo + (hi - lo)/2, hi); //找出3个数的中位数的指针，设为基准点
    swap(a, lo, m); //交换左端点和中位数
    
    int j = partition(a, lo, hi);
    sort(a, lo, j-1);
    sort(a, j+1, hi);
}

经验证可以使Quick sort速度平均提升10%

Ref: Quick Selection 快速选择

即找出一个大小为N的数组中第K小的数组，e.g. K=0即最小值，K=N即最大值，K=N/2即中位数

解决方案：利用quick sort的一种变体，即对数组进行分区：
(1)假设基准点的位置刚好为K，则输出基准点j的值
(2)如果基准点j的位置在K左边，则对右半分区继续分区，然后循环(1)(2)(3)
(3)如果基准点j的位置在K右边，则对左半分区继续分区，然后循环(1)(2)(3)
重复(1)(2)(3)直到基准点刚好为K

1
2
3
4
5
6
7
8
9
10
11
public static Comparable select(Comparable[] a, int k) {
    StdRandom.shuffle(a); //对数组进行洗牌
    int lo = 0, hi = a.length - 1;
    while (hi > lo) {
        int j = partition(a, lo, hi); //分区
        if      (j < k) lo = j + 1; //(2)
        else if (j > k) hi = j - 1; //(3)
        else            return a[k]; //(1)如果基准点位置为K,则输出基准点的值
    }
    return a[k];
}
Complexity

Time: ~N (linear time)
分析：
Best Case: 每次分区后，剩余的数组为原来的一半，即需要N+N/2+N/4+N/8+…+1 ~2N
Worst Case: 同quick sort，需要进行N次分区，第i次分区需要N-i次比较，共$1/2N^2$ (因此需要进行洗牌避免)

Ref: Three-way Partitioning

假设数组中存在很多相同元素，使用原始的quick sort会导致quadratic的复杂度，
(假设数组元素全部相同，则每次递归进行i次比较而不进行交换，一共N次递归，复杂度为worst case的$1/2N^2$)

因此我们需要实现另一种partition，将数组分为三个区间，
将所有与基准点相同的元素一起放在数组中间分区，左边是全部小于基准点的元素，右边是全部大于基准点的元素：

小于v的元素（左区间） v, v, v, …, v （基准点区间） 大于v的元素（右区间）
  1. 除了数组的左右边界lo和hi外，还需要3个指针，其中：
    i指针从左端点往右移动，直到和gt指针交叉
    lt指针从左往右移动，为基准点区间的起点（lt指针左边的元素为左区间）
    gt指针从右往左移动，为基准点区间的终点（gt指针右边的元素为右区间）
  2. 从左往右，每移动i指针一位，进行以下操作(v为基准点的值)：
    2.1 如果a[i] < v，则交换a[lt]和a[i]，并对指针i和lt加1 (把小于基准点的值移到左区间)
    2.2 如果a[i] > v，则交换a[gt]和a[i]，并对指针gt减1 (把大于基准点的值移到右区间)
    2.3 如果a[i] == v，则对指针i加1 (不需要任何移动) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private static void sort(Comparable[] a, int lo, int hi){
    if (hi <= lo) return;
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo;
    while (i <= gt) {
        int cmp = a[i].compareTo(v);
        if (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else i++;
    }
    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

Ref: Java Comparator

用于数组排序：
Comparable接口只实现了某种数据类型唯一一种total order的比较大小方式，
如果我们希望某种数据类型能够基于不同方式进行大小比较并排序，则需要实现comparator接口：
e.g. 我们设计一个student的数据类型，里面有name和section两个变量。
如果我们想要student类型的数据按照name变量来排序，则需要实现一个名为ByName的内部接口类：

1
2
3
4
5
6
//...外面是名为Student的Class
private static class ByName implements Comparator<Student> {
    public int compare(Student v, Student w) {
        return v.name.compareTo(w.name);
    } 
}

Comparator接口需要定义一个compare方法，用于告诉java系统如何比较两个数据的大小
然后我们可以生成一个comparator实例用于排序，这里可以用预先定义的方法生成，也可以用调用函数的方法生成：

1
2
3
4
5
6
7
8
9
//假设有一个数据类型为Student的数组a

//预先定义式，可以通过Arrays.sort(a, Student.BY_NAME); 调用并对a数组排序
public Comparator<Student> BY_NAME = new ByName();

//函数式，可以通过Arrays.sort(a, a[0].getByNameComparator())；调用
public Comparator<Student> getByNameComparator() {
    return new ByName();
}

一种数据类型可以既实现Comparable接口，又可以在内部实现Comparator接口并生成Comparator实例

Ref: Stability

假设一列数据有多个key，用排序算法对其某个key进行排序
一个排序算法是stable的，即对当key的值相同的元素进行排序时，不影响其他key的相对顺序
（即假设key1已经是排好序的，对key2进行排序，在key2相同的元素中同样也按key1排好序）

目前已知的stable算法：insertion和merge

排序算法总结

Algorithms inplace? stable? worst average best remark
selection yes $N^2/2$ $N^2/2$ $N^2/2$ N exchange
insertion yes yes $N^2/2$ $N^2/4$ $N$ 常用于当N比较小或数组已经部分排好序（近乎线性复杂度）
shell yes $N^{1.5}$ $N^{1.3}$ N subquadratic
merge yes $NlgN$ $NlgN$ $NlgN$ $NlgN$ guarantee, stable
quick yes $N^2/2$ $2NlnN$ $NlgN$ $NlgN$ probabilistic guarantee，目前实践中最快的算法
3-way quick yes $N^2/2$ $2NlnN$ $N$ 改进的quick sort，适应duplicate key
Heap yes $2NlgN$ $2NlgN$ $NlgN$ $NlgN$ guarantee, in-place

Week 4. Priority Queue / Heap 优先队列 / 堆

定义，有序的队列，即每次删除操作只删除最大或最小值

API

(e.g. Max Priority Queue, 每次删除最大值)

1
2
3
4
5
6
7
8
9
// 注意：与一般Queue相比，我们希望MaxPQ里面的元素是comparable的，以便在队内进行排序操作
public class MaxPQ <key extends Comparable<Key>> {
    MaxPQ()                 // create an empty priority queue
    MaxPQ(Key[] a)          // create an priority queue with given keys
    void insert(key v)      // return and remove the largest key
    boolean isEmpty()       // is the priority queue empty
    key max()               // return the largest key
    int size()              // number of the entries in the priority queue
}
最简单的两种Priority Queue实现
  1. (Unordered PQ) 每次将元素插入到队列末端，每次删除需要遍历整个Queue找出最小值
    –插入需要O(1), 删除需要O(N)，查找最值需要O(N)
  2. (Ordered PQ) 每次插入需要插入到合适位置使queue始终有序，删除操作只需删除队尾元素
    –插入需要O(N)，删除需要O(1)，查找最值需要O(1), 分为链表和数组两种实现
    两种都需要O(N)时间复杂度

Binary Heap

1. Complete Binary Tree
  1. Binary Tree二叉树：一个节点连接两个左右子二叉树，或者节点为空的树
  2. Complete Binary Tree完全二叉树：整个树除了底层节点外，每个节点都有两个子节点
    一个有N个节点的 CBT的层数为floor(lgN)
2. Binary Heap

即数组形式表现的Complete Binary Tree
如何将CBT存储为数组形式？

  1. 按照层遍历(BST)完全二叉树，并依次分配一个递增的索引index（index start from 1）
  2. 按照分配的索引放入数组a的对应位置
    (以上称为Heap Ordering 堆排序，即父节点的index一定小于子节点的index，同一层左边的节点index小于右边的)

通过数组形式存储，我们就无须实际生成整个完全二叉树，通过数组操作实现堆操作

3. Properties
  1. index=1 (a[1]) 对应的元素为所有元素的最大值，即根节点为最大值
  2. index为k的节点的父节点index为k/2，子节点index为2k和2k+1 （因此我们需要index从1开始）
  3. 父节点需要大于（MaxPQ）或小于（MinPQ）其子节点

通过性质2我们可以很方便的通过数组访问CBT的节点

4. Eliminate the Violation

e.g. (以MaxPQ为例，即堆元素从上往下减小)

Case 1: Promotion
前提假设：我们改变一个节点的值，使其大于父节点的值
方法：我们可以将其与父节点交换，交换后再将该节点与新的父节点相比较，层层向上交换直到根节点
(Peter Principle: node promoted to level of incompetence，类似于升职过程)

1
2
3
4
5
6
private void swim(int k) {
    while (k > 1 && less(k/2, k)) {
        exch(k, k/2);
        k = k/2;
    }
}

Case 2: Demotion
前提假设：我们改变一个节点的值，使其小于其两个子节点
方法：我们将该节点与它最大的子节点交换，交换后再将该节点与新的子节点相比较，层层向下交换直到叶子节点
(Power Struggle: Better subordinate promote，类似于降职过程)

1
2
3
4
5
6
7
8
9
private void sink(int k) {
    while (2*k <= N) {
        int j = 2*k;
        if (j < N && less(j, j+1)) j++; // find the maximum child node
        if (!less(k, j)) break; // legal position
        exch(k, j);
        k = j;
    }
}
5. Insert

基于4的Promotion原理，对于新插入的元素，我们可以将其直接插入到数组尾端（即树的叶子节点），然后判断这个新插入的节点是否violation

1
2
3
4
public void insert(Key x) {
    pq[++N] = x;
    swim(N);
}

该操作复杂度为logN，即我们只需要最多1 + floor(lgN)次compare

6. Delete the Max

基于5的Demotion原理，我们用数组中最后一个元素（即最小值）替换掉堆顶元素（即根节点最大值），然后对新的堆顶元素做Demotion操作

1
2
3
4
5
6
7
public Key delMax() {
    Key max = pq[1];
    exch(1, N--);
    pq[N+1] = null; // prevent loitering 记得把最后一个节点设为null
    sink(1);
    return max;
}

该操作复杂度为logN

7. Total Complexity: O(lgN)

Insert: O(lgN); Delete: O(lgN); Max: O(1)

8. Other Notice
  1. 我们不希望client能够随意改动已经放入PQ的Key，因此实现特定数据结构Key时需要 a. 对整个class声明final，即public final class Key{} b.对数据结构内部所有变量需要设置为private final c. 这个数据类型中所有可调用的方法都不能改变内部变量的值
    (Some Immutable Variable: String, Integer, Double;
    Some Mutable Variable: StringBuilder, Stack, Counter, Java array)

HeapSort 堆排序

即利用堆顶元素最大的原理，将待排序的元素建立一个堆，每次提取堆顶元素再建立新堆，直到所有元素都提取完成

Implementation

假设存在一个数组a[N]需要排序

  1. 我们将a[N]按照heap order排序，即用这些数据建立一个max heap最大堆
  2. 当我们获得堆后，堆顶元素即为最大值，将其与数组最后一个元素（即第N个元素）交换。
    设置一个指针i=N指向第N个元素，表示这个元素以及之后的元素是排好序的，剩余堆为[1, i-1]。
    对堆顶元素进行sink操作直到整个剩余堆[1,i-1]是valid的，
  3. 重复操作2，每次将堆顶元素放入已排好序区间的开头位置，同时移动指针i–，使得这个数组的前面一部分[1, i-1]是堆，后面一部分[i, N]是部分排好序的数组

注意：为了实现in-place，我们直接在原数组上建堆，即我们从后往前，对每个节点进行sink操作以确保局部堆的合法性。即我们确保了两个局部堆是valid的，然后通过sink两个堆的父节点来确保这两个堆合并为一个大堆后是valid的
（实际上第N/2 + 1到第N个元素都是没有子节点的，我们可以直接从第N/2个元素开始）
为什么不从前往后建堆：因为所有的insert或者sink操作，前提是需要这个堆除了这个元素外其他都是in heap order的，否则通过sink操作并不能得到valid的堆；从后往前建堆以保证每个子堆vaild以及merge后也是valid的

1
2
3
4
5
6
7
8
public static void sort(Comparable[] a) {
    int N = a.length;
    for (int k = N/2; k >= 1; k--) sink(a, k, N); // Step 1：in-place heap builder
    while (N > 1) { // Step 2: put the largest element to the right and rebuild the heap
        exch(a, 1, N);
        sink(a, 1, --N);
    }
}

（注意这里我们的数组index是从0开始到N-1，而使用PQ的index是从1到N，因此我们需要在进行exch和sink操作时将两种索引进行对应的转换）

Complexity: ~NlogN

唯一能保证worst case为NlogN的in-place算法
（Mergesort：non in-place；Quick Sort：worst case ~N^2）

补充：为什么在industry中不常用HeapSort：

  1. 其他sort访问元素都是比较连续的局部顺序访问，而HeapSort经常会需要访问数组中两个距离较远的元素（比如访问子节点依次需要访问1，2，4，8，…等相距的节点），使得CPU需要较大缓存cache（CPU缓存可能一次只能从内存中读取小部分数组，访问其他块的元素需要多次内存<->缓存操作），导致效率变低
  2. HeapSort需要的交换次数多于Quick Sort，因为每次建堆过程(insert / delete)都会打乱Heap Order，以致数据有序度降低
  3. 不是Stable的算法 （区别Merge Sort）

Week 5. Symbol Table 符号表

符号表主要目的就是将一个键（Key）和一个值（value）关联起来，可以将一个键值对（Key-Value Pair）插入到符号表中并能够通过key直接找到对应的value

API

1
2
3
4
5
6
7
8
9
10
public class ST<Key, Value> {
    ST(); // 创建一个符号表
    void put(Key key, Value val); // 存储键值对
    Value get(Key key); // 获得key对应的value
    void delete(Key key); // 删去key及对应的value
    boolean contains(Key key); // 判断ST是否包括key
    boolean isEmpty(); // 判断ST是否为空
    int size(); // 获取ST中的键值对数量
    Iterable<Key> keys(); // 遍历表中的所有key
}
Limitation

关于null值的几个限定：

  1. value不能为null
  2. 当key不存在时，get(key) 方法返回null
  3. 当key存在时，put(key, value)方法将覆盖旧的value
补充：contains和delete方法的实现
1
2
3
4
5
6
7
// 对于所有的ST，contains方法都是相同的
public boolean contains(Key key)
{return get(key) != null; }

// 一种简单的delete方法（仅对某些实现有效）
public void delete(Key key)
{put(key, null);  }
补充：Java Equality Test (相等性测试)

所有的java class内部都包含equals()函数，用于测试两个对象是否相等
判断对象相等的标准：

  1. Reflexive 自反性：x.equals(x) == true
  2. Symmetric 对称性：x.equals(y) iff y.equals(x)
  3. Transitive 传递性：x.equals(y) & y.equals(z) => x.equals(z)
  4. Non-null 非空：x.equals(null) == false

equals实现方法：

  1. Java默认实现：x == y （即判断两个对象的地址是否相同，较不常用）
  2. 自定义(即根据不同对象类型自行设计各种判断来实现equals函数，注意需要满足上述四大标准)
    e.g. 假设我们有个Date类，里面有(int month, int day, int year)三个值，需要实现equals函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public boolean equals(Object y) { // 注意这里，java规范规定传入类型必须为Object而非自定义的类

    if (y == this) return true; // 优化：如果两个对象地址相同，则一定相等
    
    if (y == null) return false; // 判断Non-null非空（标准4）
    
    if (y.getClass() != this.getClass()) return false; // 两个对象的类相同，两个对象才相同
    Date that = (Date) y; // 经过上面判断后，cast操作一定成功
    
    // 上面的代码对任何equals函数都是必要的
    
    // 比较各个field的逻辑
    if (this.day != that.day ) return false;
    if (this.month != that.month) return false;
    if (this.year != that.year ) return false;
    return true;
    
    // 对于字段field的比较方法（上面的day，month和year）
    // 1. 如果field为基本数据类型primitive type，则直接用==比较
    // 2. 如果field为object类型，则用该object的equals函数进行比较
    // 3. 如果field为数组，则我们需要遍历数组并对数组中的每一项进行equals比较
    //      (可以采用Arrays.equals(a, b)或者Arrays.deepEquals(a, b) （适用于多维或嵌套数组），
    //      但不能采用a.equals(b))
}

两种简单的ST实现

1. 无序链表

键值对为链表的一个节点
search：从头至尾遍历链表，直到找到对应的key => O(n)
insert：每次插入先serach对应的key是否存在于链表中，如果不存在则直接插入到链表头部 => O(n)
注意:
这种实现只需通过equals()函数比较key而无需通过compareTo()进行key排序，但也无法顺序输出键值对

2. 顺序数组 + 二分查找

需要两个并行数组keys和values来分开存储key和value
search：通过二分查找函数rank()来获取key在keys数组中的索引i，并以此索引i来获得value = values[i]，如果未找到对应的key则返回null => O(logN)
insert：通过rank()函数找到对应插入的位置i，对keys和values数组将i后面的所有元素往后移动一位，再将key-value插入到对应位置；如果key存在则直接改写对应的value值 => O(N)
注意：和无序链表实现相比，需要通过compareTo()函数实现二分查找，同时可以顺序输出键值对

补充：当key是comparable时，还可以有其他应用（统称为ordered operations）：

  1. 找到最小或最大的key （min()和max()函数）或者删除最大或最小值(deleteMin()和deleteMax()函数)
  2. 查找特定位置的key(select()函数)
  3. 找到最接近的key(ceiling()和flooring()函数)
  4. 获得key在ST表中的顺位(rank()函数)
  5. 迭代ST表

Binary Search Tree 二叉查找树

定义

每个节点有一个key值，每个节点的key值大于这个节点的左子树中所有节点的key值，小于这个节点右子树中所有节点的key值

每个node有四个field：key，value，left，right

1
2
3
4
5
6
7
8
9
private class Node {
    private Key key;
    private Value val;
    private Node left, right;
    public Node(Key key, Value val) {
        this.key = key;
        this.val = val; 
    }
}
特征

与quick sort的关联：和quick sort一样有一个partition的过程，因此BST的inorder是有序的

查找key对应的value
1
2
3
4
5
6
7
8
9
10
public Value get(Key key) {
    Node x = root;
    while (x != null) {
        int cmp = key.compareTo(x.key);
        if (cmp < 0) x = x.left; 
        else if (cmp > 0) x = x.right; 
        else if (cmp == 0) return x.val;
    }
    return null;
}

复杂度：key所在的节点深度+1（Average: ~2lnN，由quick sort启发得来）

插入一个key-value pair
1
2
3
4
5
6
7
8
9
10
11
public void put(Key key, Value val)
{  root = put(root, key, val);  // re-link }

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val);
    int cmp = key.compareTo(x.key);
    if (cmp < 0) x.left = put(x.left, key, val);
    else if (cmp > 0) x.right = put(x.right, key, val);
    else if (cmp == 0) x.val = val;
    return x; // tricky part：注意这里我们虽然返回的是一个节点，但我们需要把他想象成一个link，让其父节点连接到这个修改后的子树
}

复杂度：key所在的节点深度+1 （Average: ~2lnN）
补充：二叉树的形状，取决于节点插入的顺序
如果二叉树的节点是按顺序插入的，则二叉树呈一斜线，此时二叉树的高度最大 (worst case)，等同于一个linkedlist
Average Height: ~4.311lnN (随机顺序插入情况下)

删除一个key-value pair
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void delete(Key key)
{  root = delete(root, key);  }

private Node delete(Node x, Key key) {
    if (x == null) return null;
    int cmp = key.compareTo(x.key);
    if (cmp < 0) x.left = delete(x.left, key);
    else if (cmp > 0) x.right = delete(x.right, key);
    else { // 找到要删除的节点
        if (x.right == null) return x.left; // 没有左子树，直接返回右子树
        if (x.left == null) return x.right; // 没有右子树，直接返回左子树
        // 找出右子树的最小节点来替换该节点
        Node t = x;
        x = min(t.right); // 找出右子树的最小节点替换该节点
        x.right = deleteMin(t.right); // 删掉这个最小节点（因为要替换到该节点的位置）
        x.left = t.left; // 将旧节点的左子树附到新节点的左子树上
    }
    x.count = size(x.left) + size(x.right) + 1; // 更新该节点的size()
    return x;
}

复杂度：sqrt(N)
这种删除方法存在一个问题，因为我们总是将右子树的最小值替换到删除的节点，因此当长时间进行动态的insert和delete操作后，树变得不再balance而会偏向一边（左边），导致后面的insert、search和delete操作的复杂度变为比lgN更大的sqrt(N)
该问题目前无解，即使是随机的选取左子树的最大值或者右子树的最小值替换删除的节点，复杂度仍为sqrt(N)
另外如果delete操作是order的，也会导致BST变为完全不平衡的树（因此引入红黑树解决此问题，后续会讲）

Ordered Operations

min() / max(): 一直递归左子树直到叶节点即为最小值；一直递归右子树直到叶节点即为最大值
floor()：找出比该key小的所有节点的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public Key floor(Key key) {
    Node x = floor(root, key); if (x == null) return null; return x.key;
}

private Node floor(Node x, Key key) {
    if (x == null) return null;
    int cmp = key.compareTo(x.key); 
    if (cmp == 0) return x; // 找到exact same的值，直接返回节点
    if (cmp < 0) return floor(x.left, key); //当前节点比key大，说明target肯定在该节点的左子树中
    Node t = floor(x.right, key); if (t != null) return t;
    // 当前节点比key小，说明当前节点可能是target
    // 如果在他右子树中能发现target，则证明能找到更大的比key小的值，返回新的target
    // 否则当前节点的值就是要找的下界，直接返回
    else return x;
}

ceiling()同理类推
size()：在node节点中增加一个size field，代表该节点为根的树的大小，在插入操作时同时修改每个节点的size
rank()：利用size()函数递归操作，对于某个节点的rank，等于其左子树的size()以及其父节点的左子树的size()依次递归

Ordered Iteration

1
2
3
4
5
6
7
8
9
10
11
12
public Iterable<Key> keys() {
    Queue<Key> q = new Queue<Key>();
    inorder(root, q);
    return q;
}
// Inorder traversal: BST的中序遍历为有序的
private void inorder(Node x, Queue<Key> q){
    if (x == null) return; 
    inorder(x.left, q);
    q.enqueue(x.key);
    inorder(x.right, q);
}

复杂度：除了Ordered Iteration为N，其他ordered operation的复杂度都为h (节点的深度，avg为lgN)

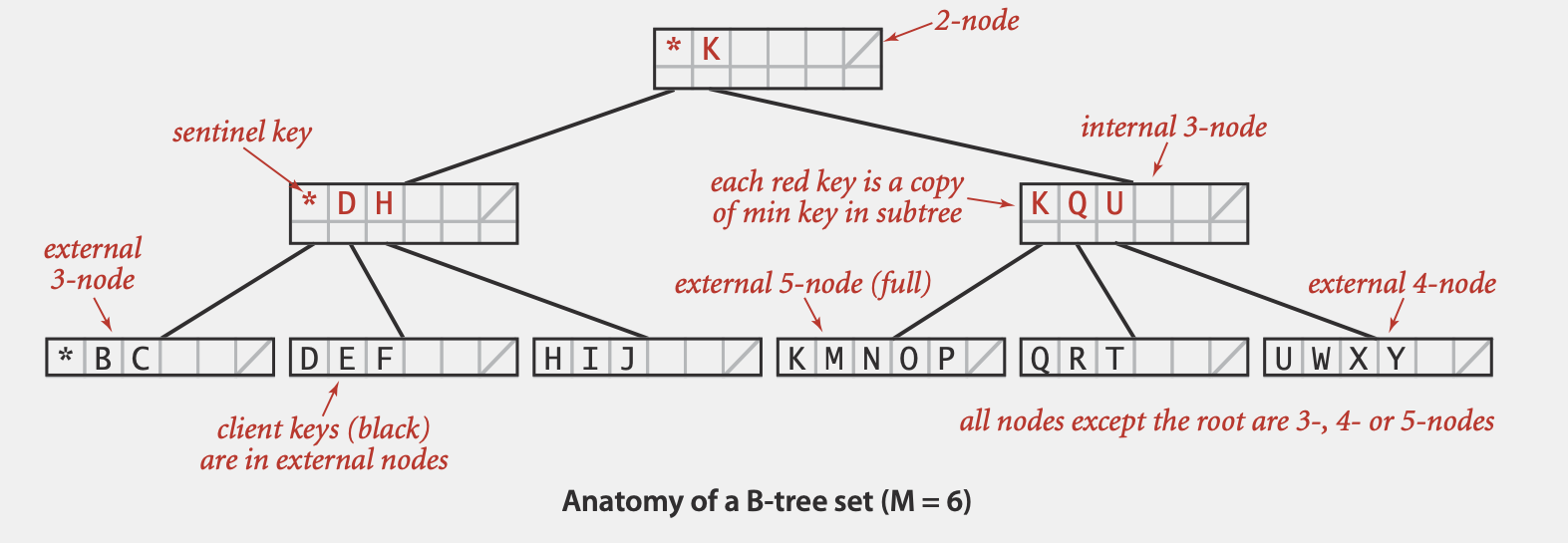
2-3 Tree

定义&特征

2-3 Tree是Balanced Search Tree的一种，每个节点可以有1个或两个key，分别称为2-node或3-node:
2-node: 包含1个key和2个子节点，其中左子树的所有节点的key小于该节点，右子树所有节点的key大于该节点
3-node: 包含2个key和3个子节点，假设该节点有两个key，分别为a和b，则有：

  1. 这个节点左子树的所有节点的key小于a
  2. 这个节点右子树的所有节点的key大于b
  3. 这个节点中子树的所有节点介于a和b之间

2-3树有如下特征：

  1. 每条从root节点到叶子节点（或null节点）路径的长度总是相等的（即Perfect Balanced）
  2. 2-3树的中序遍历也是有序的
  3. 树的高度：
    1. worst case（即全为2-node）：lgN
    2. best case（即全为3-node）：log_3 N (~0.631lgN)

基本方法和BST相同：

  1. 如果target在一个2-node或3-node里面，表示找到target
  2. 如果dfs到一个2-node且target不在里面，如果2-node的key > target则递归到左子树，反之递归到右子树
  3. 如果dfs到一个3-node且target不再里面，假设有两个key分别为a，b，如果target < a则递归到左子树，如果a < target < b则递归到中子树，如果target > b则递归到右子树
  4. 如果节点为null，代表没找到target，返回null
Insert

假设我们通过search找到key要插入的位置，为一个2-node或3-node叶子节点

  1. 假设要插入的位置为2-node，我们可以直接插入到2-node使其变为一个3-node
  2. 如果要插入的位置为3-node：
    1. 我们先将key插入到这个3-node使其变为一个临时的4-node（即含有三个key和四个子树）
    2. 然后进行split操作：将这个4-node分开成3个2-node，最左边的2-node包含了原本4-node的左边两个子树，最右边的2-node包含了原本右4-node的右边两个子树，中间的2-node将其向上合并到原本4-node的父节点
    3. 此时原本4-node的父节点可能是一个3-node，也有可能是一个4-node，如果是一个4-node，就继续进行split操作并向上合并。如果是3-node则无需进一步操作

补充：2-3树原理较为简单，但实现比较复杂，需要考虑到多种情况，这里暂时不需要掌握具体实现
另外有其他实现更简单的Balance Search Tree（e.g. 红黑树）

Complexity

所有操作都能保证为lgN的复杂度 (lgN guarantee)

(left-leaning) Red-Black BSTs

定义&特征

基本思想：2-3树因为存在2-node和3-node（尤其是3-node），因此插入和查找操作相对BST比较复杂。我们希望我们的树结构能和BST一样简单,但是又能体现出2-node和3-node。即我们需要在BST中用一种简单的方法来表现3-node

如何在BST中表现3-node？

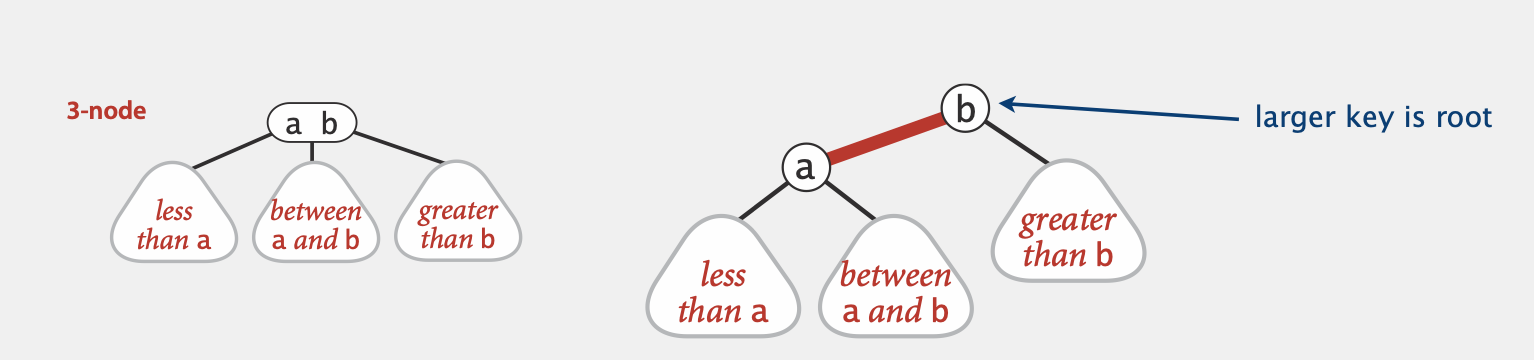
3-node.png

我们用一个称为left-leaning link（即上图红色的边）来粘结3-node，此时原本3-node的左子树为a的左子树，中子树为a的右子树，右子树为b的右子树

原本3-node中较大的key为新的BST中的根节点，我们用红色的边标记a和b之间的internal link，以示和其他link区别

e.g. 完整的2-3 Tree以及其对应的RB Tree表示

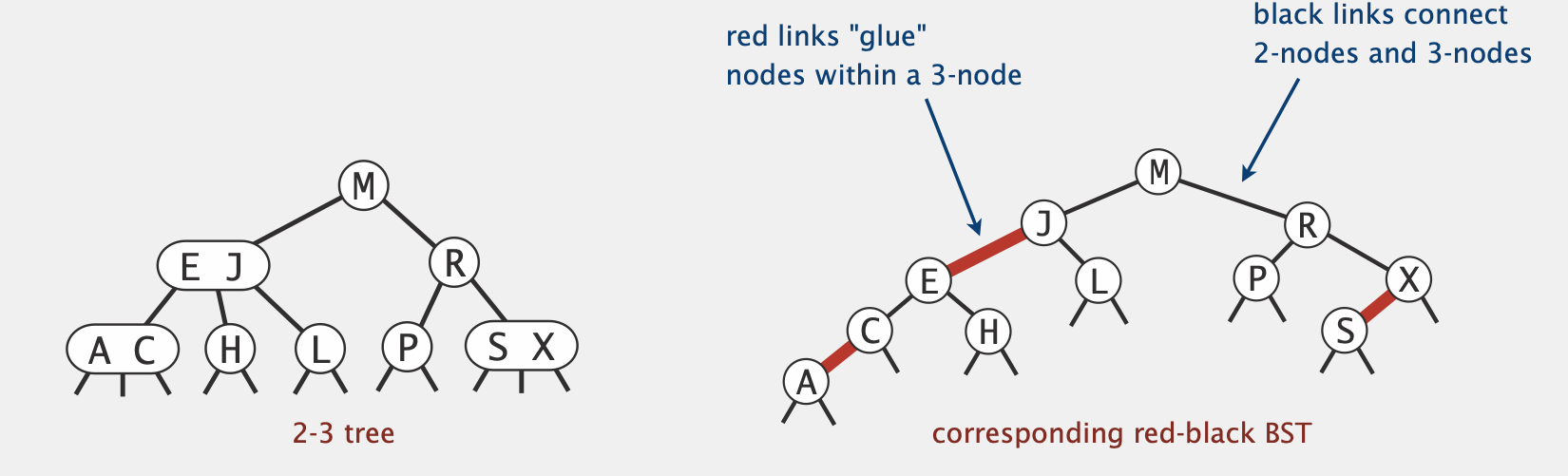
2-3 Tree.png
2-3 Tree.png

黑色的边连接原本的2-node或3-node，红色的边为internal link，用来表现3-node

红黑树定义：

  1. 任何节点不会有两个红色的边与其相连

  2. 任何从根节点到叶子节点（或null节点）的路径所包括的黑色的边的数量相同 （黑色边连接2-node和3-node，原先2-3树中每条路径的节点数相同，对应红黑树的黑边数量相同）

  3. 所有红色的边都是向左的，称为left-leaning

Search & other ordered ops

Search操作以及其他ordered ops和BST是完全一样的，但由于树的平衡性更好，因而效率更高

Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private static final boolean RED   = true;
private static final boolean BLACK = false;

private class Node {
   Key key;
   Value val;
   Node left, right;
   boolean color; // color of parent link
}

private boolean isRed(Node x) {
   if (x == null) return false;
	return x.color == RED; 
}

在BST节点的基础上增加一个color field，用来表示这个节点连接到其父节点的边颜色

（上图中，A, E, S节点的color为RED而其他node为BLACK）

补充：我们默认所有null节点都是黑色的（因为它不可能是3-node中的key）

Basic Operations Required For Insertion

在实现insertion 操作之前，我们需要实现两个基本的rotation操作，使得将一个right-leaning的3-node变成left-leaning，或者将一个left-leaning的3-node临时变成right-leaning（再变回left-leaning）。还需要一个等效于原来4-node分裂成2-node的操作。后续Insertion操作会用到这些操作

  1. Rotate Left
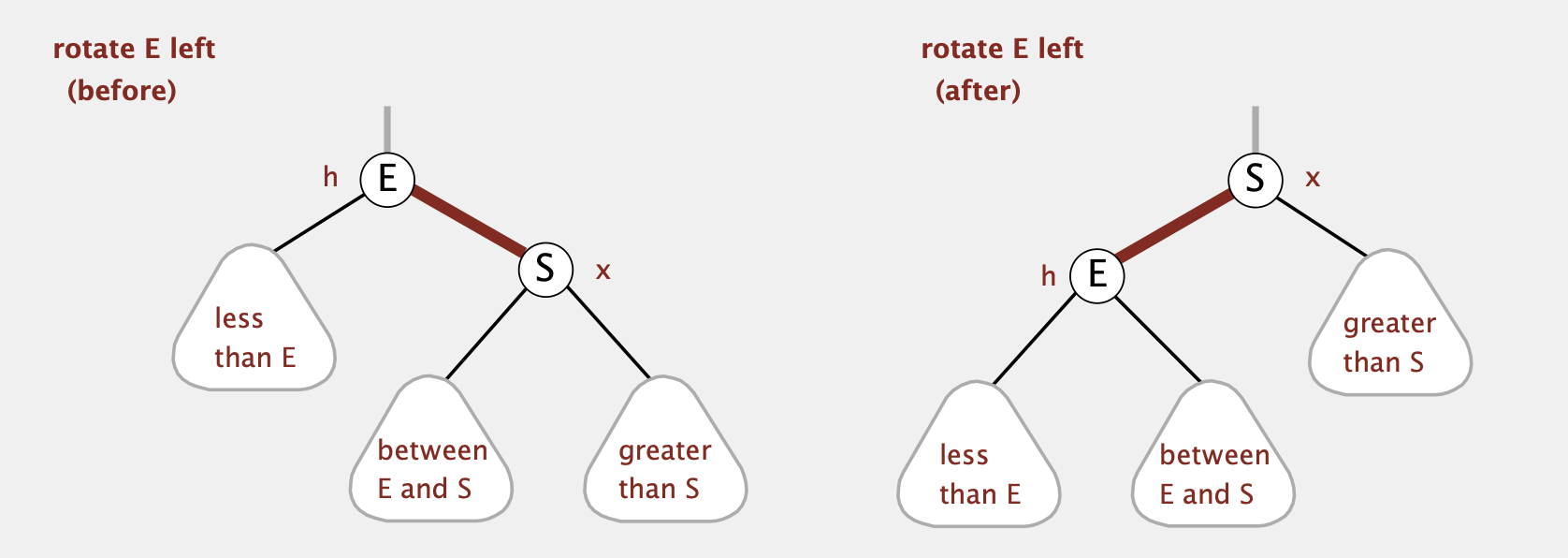
rotateLeft.png
rotateLeft.png

假设h节点的右节点为红色（即leaning-right），rotate之后x将成为新的父节点并返回。剩余的三棵子树中，原来的左子树和右子树都不用变（还是连接在原来的h和x节点上），中子树需要从原来x节点的左子树连接到h节点的右子树

1
2
3
4
5
6
7
8
9
private Node rotateLeft(Node h) {
    assert isRed(h.right);
    Node x = h.right; // 先保存x
    h.right = x.left; // 将中子树从x连接到h上
    x.left = h; // 旋转，将h连接到x左边（变为left-leaning）
    x.color = h.color; //同时需要改变两个节点的颜色
    h.color = RED;
    return x; // 返回旋转后新的3-node根节点
}

  1. Rotate Right

    原理同Rotate Left，先调整中子树再rotate

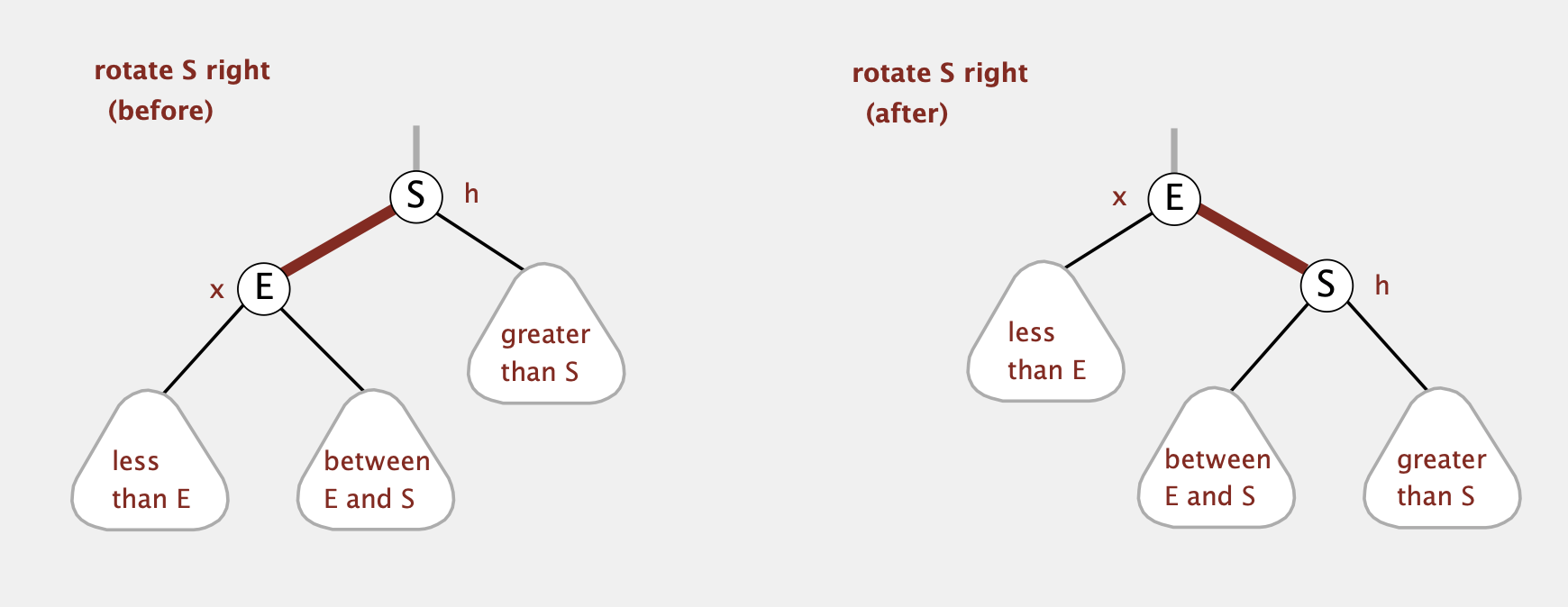
rotateRight.png
rotateRight.png
1
2
3
4
5
6
7
8
9
private Node rotateRight(Node h) {
    assert isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color; // 注意这里，我们希望旋转之后除了这个3-node之外整个树其他部分都不变化（包括其他各边的颜色），因此这里我们新的根节点的颜色（即这个node连接到上面父节点的边的颜色）选择与原来一样保持不变
    h.color = RED;
    return x;
}
  1. Color Flip
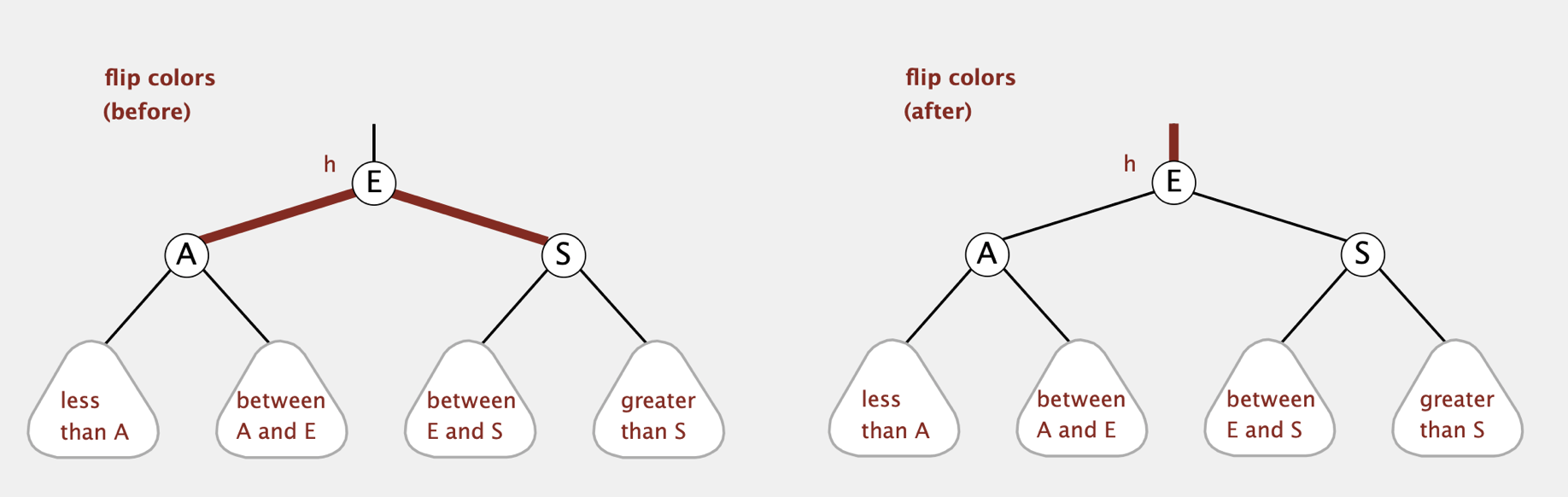
colorFlip.png
colorFlip.png

在insert的过程中可能会遇到一个节点的两个子节点都是Red节点（等价于原来的4-node）。此时我们需要将其分为两个2-node（即图中的A和S节点），并将表示中间key的节点（图中的E）向上移动。

将4-node分为2个2-node，可以直接将两个红色节点设为黑色即可

对中间节点（E节点）的颜色进行分类讨论：

  1. 假设E的父节点表示的是一个2-node（即只有一个key），则直接将E设为红色节点可以使这个2-node变为一个3-node。即使我们不知道E是左节点还是右节点，我们也可以通过旋转操作进行调整

  2. 假设E的父节点表示的是一个3-node，则将E设为红色后，E的父节点将有两个红色节点，此时等价于左图中的4-node情况，需要继续进行color flip

    因此我们直接将4-node的中间节点设为红色，左右节点设为黑色即可 (只需设置相应节点的颜色而无需更改link)

1
2
3
4
5
6
7
8
private void flipColors(Node h) {
    assert !isRed(h);
    assert isRed(h.left);
    assert isRed(h.right);
    h.color = RED;
    h.left.color = BLACK;
    h.right.color = BLACK;
}
Insertion

基本策略：通过上面的rotation和color flip，实现与2-3 Tree insertion一一对应的等价操作

  1. 按照search方法找到插入位置后，我们将要插入的节点设为红色并插入到对应位置（即将原本的2-node变为3-node或原本的3-node变为4-node，因而设为红色）

  2. 如果插入后的link是right-leaning的，我们通过left-rotation使其变为left-leaning的合法RBT

  3. 如果插入后，使得存在两个连续的边（下图两种情况）

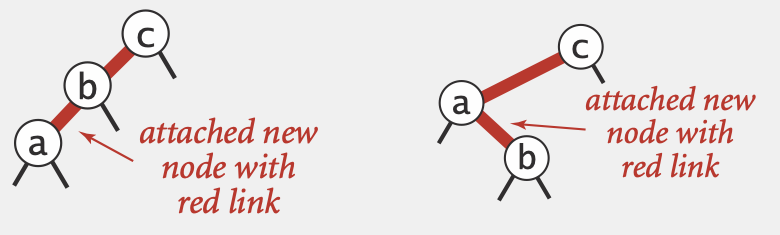
    2-leanLeft.png

    左图情况下，直接以c为节点进行rotateRight使其变为一个4-node，再进行color Flip

    右图情况下，因为a节点会比b节点优先检查到，在检查a节点时会进行第二步的left-rotate操作使其变为左图情况

    （补充第另外两种种右左情况和右右情况，因为先检查是否存在right-leaning，因此进行left-rotate后都会变为上面两种情况，因此实际上不会存在）

    因此任意两个node插入第三个node，最终都会归结到左图情况，进行rotateLeft再color flip即可

  4. 插入后依次向上对每个节点进行合法性检查，最终得到合法RBT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private Node put(Node h, Key key, Value val) {
    // BST插入部分（同一般BST插入）
    if (h == null) return new Node(key, val, RED);
    int cmp = key.compareTo(h.key);
    if (cmp < 0) h.left = put(h.left, key, val);
    else if (cmp > 0) h.right = put(h.right, key, val);
    else if (cmp == 0) h.val = val;

    // 检查每个节点是否合法：调整节点使其成为合法RBT
    if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);//此时该节点是leaning-right的，直接左旋
    if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);//上面case3, 等价于生成4-node
    if (isRed(h.left) && isRed(h.right)) flipColors(h); //split 4-node
    return h;
}

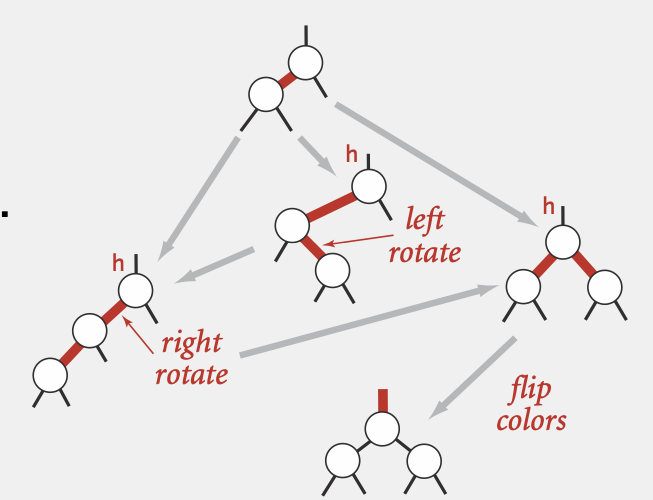
状态转换过程: 对每个非法节点进行一步步的状态转换（一共三种状态），直到转换为合法状态

caseTransfer.png
Complexity

Tree Height: <= 2lgN in worst case (每条路径的黑边数相同，且没有两条连续的红边，假设worst case最坏情况是一条黑边一条红边交错相连，因而worst case为2lgN)；1.00lgN in average case；

Time Complexity: 2lgN in worst case and lgN in average case for all operations.

（Optional）B-Tree

Defination

B-树是Blanced Search Tree在文件系统中的应用。通常我们需要存储大量文件和数据在external storage中，需要尽可能快的查找到所需的文件

基于2-3树，B-Tree一个节点设置为可以包含最多M个key（M往往很大，e.g. 1024）和M-1个link （而2-3树中每个节点只能包括1个或2个key）。B-Tree还有如下性质

  1. root节点至少要有两个key
  2. 其他节点至少要有M/2个key （我们不希望每个节点太空，以保证查找高度不会太高）
  3. 所有的数据都存储在external node（外部节点，即叶节点）中，只存储数据的key且从左到右有序排列
  4. B-Tree的internal node（内部节点，即非叶节点）仅用于搜索而非存储数据和key
  5. 当节点填满后，将一分为两个节点，并在其父节点添加一个新key
BTree.png
BTree.png
Complexity

log_{M-1} N 到 log{M/2} N，for all operations

（每个节点包含的边的数量总是在 M/2 到 M-1之间）

Avg：当M = 1024 & N = 62 billion, log {M/2} N <= 4，即探查次数不超过4次

Geometric Application

在ST的基础上增加两个函数：

  1. Range Search：找出所有大小介于k1和k2之间的key
  2. Range Count：找出所有大小介于k1和k2之间的key的数量

如果将所有key排列成一条直线（即1维状况），上面两个操作等同于找出这题直线某个区间内的所有点

BST Implementation：

  1. count：使用rank函数，找出两个key的rank，两者之差的绝对值即为结果
  2. search：中序递归，先递归查找左子树中是否包含在两个key之间的key，再检查当前key，再递归查找右子树是否包含在两个key之间的key

Time Complexity:

data structure Insert range count range search
unordered list 1 N N
ordered array N logN R + logN
BST logN logN R + logN

N = number of keys

R = number of keys that match

1D Range Search的应用: Orthogonal line segment intersection

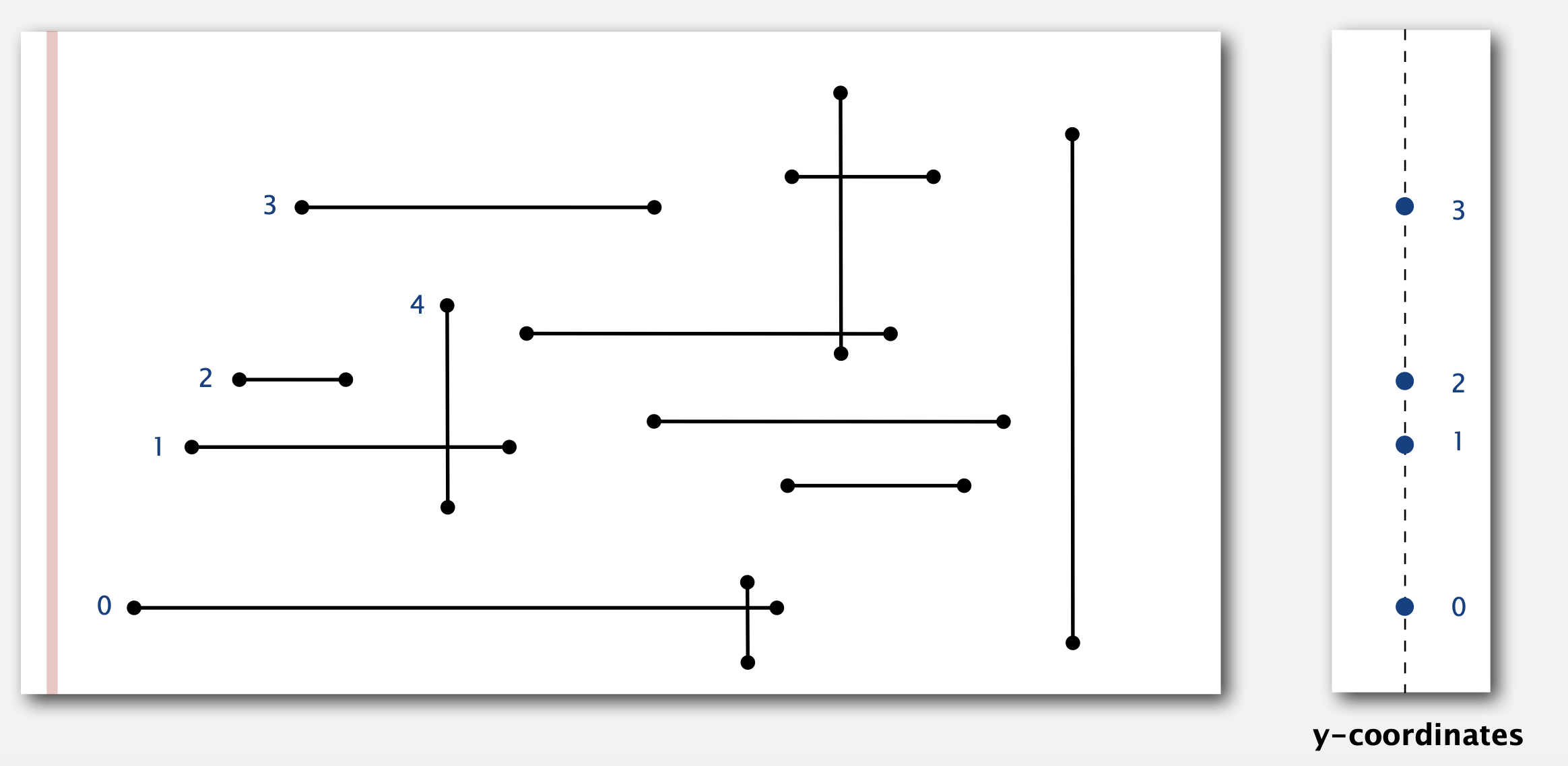
Orthogonal line segment intersection.png
Orthogonal line segment intersection.png

如图，平面中有许多水平线和垂直线。我们需要找出所有的交点。不存在任何重合的直线。

方法 （Sweep-line Algorithm，线段扫描算法）：

  1. 图中红色的线从左到右依次扫描。遇到一条水平线的左端点后，将这条线的y坐标插入到BST中 （图中按0，1，2，3顺序依次插入）
  2. 遇到一条垂直线的右端点，则将该线的y坐标从BST中移出（移出2）
  3. 遇到垂直线后，假设这个垂直线两端点的y坐标分别为y1和y2，对BST进行Range Search(y1, y2)可以找到与该垂线相交的直线数量（e.g. 搜索线段4在BST中的range可以得到1的y坐标在range范围内，即与线段4相交的线段数量为1）

时间复杂度：NlogN （每条线需要logN复杂度的BST操作，一共N条线）

即我们假设每个key有K个维度，通过KD-Tree我们可以搜索给定维度范围内的key

e.g. 假设二维空间内有一群数据点，每个数据点包括两个field，如一个人的收入和年龄。我们可以通过一个2-D正交搜索（2-D Orthonogal Range Search）来查找给定收入和年龄范围内（e.g. 100K < income < 200K, 25 < age < 40）的所有数据点（等价于查找二维平面内用一个长方形框住的所有点）

Grid Implementation

Steps

  1. 将二维空间分为M*M个网格
  2. 将每个网格中的点分别存储到对应的list中
  3. 用一个2-D数组来索引每个网格的list
  4. 对于插入操作，利用索引将点直接插入到对应的网格的点list中
  5. 对于range search操作，对于给出的2-d range query，我们找到在这个范围内的所有square，提取出对应square的所有点，再一一检查每个点是否在给定的2-d range query范围内
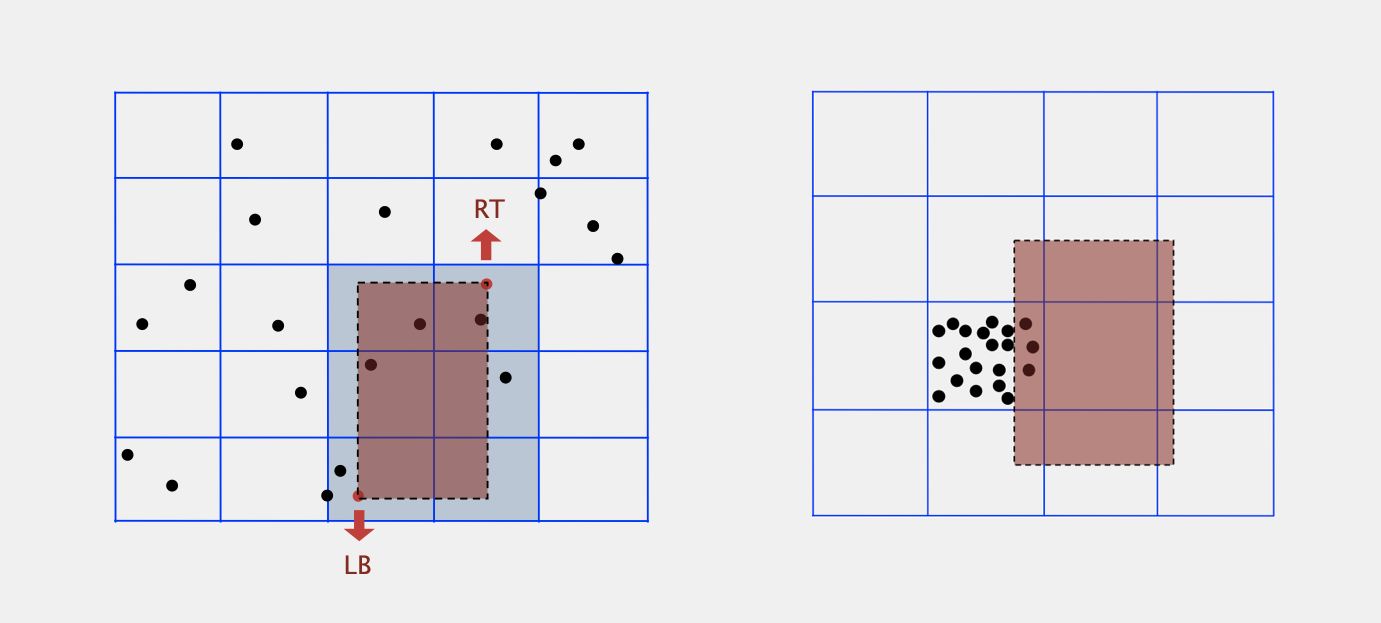
2DRangeSearch.png

Complexity

Space：M^2 + N (M^2个索引，以及需要用M^2个list存储所有N个点)

Time：对于每个examined的网格需要平均N/M^2次检查（平均每个网格包含N/M^2个点）

因此对于划分的网格大小M如果过大会导致空间复杂度上升，过小会导致时间复杂度上升（即space-time tradeoff）。

一般我们选择M = sqrt(N)，如果数据是evenly distributed的，则初始化索引的复杂度为N（sqrt(N) ^ 2）；insert的复杂度为1，range search的复杂度为1（每个网格平均包含一个点）

Issue

通常情况下，数据往往不是evenly distributed而是clustering（即大部分数据都集中在某一片区域，见上图右），导致存在少数很长的list和大多数很空的list（range search复杂度增大至趋近于N），因此需要其他数据结构

2-D Tree

Example

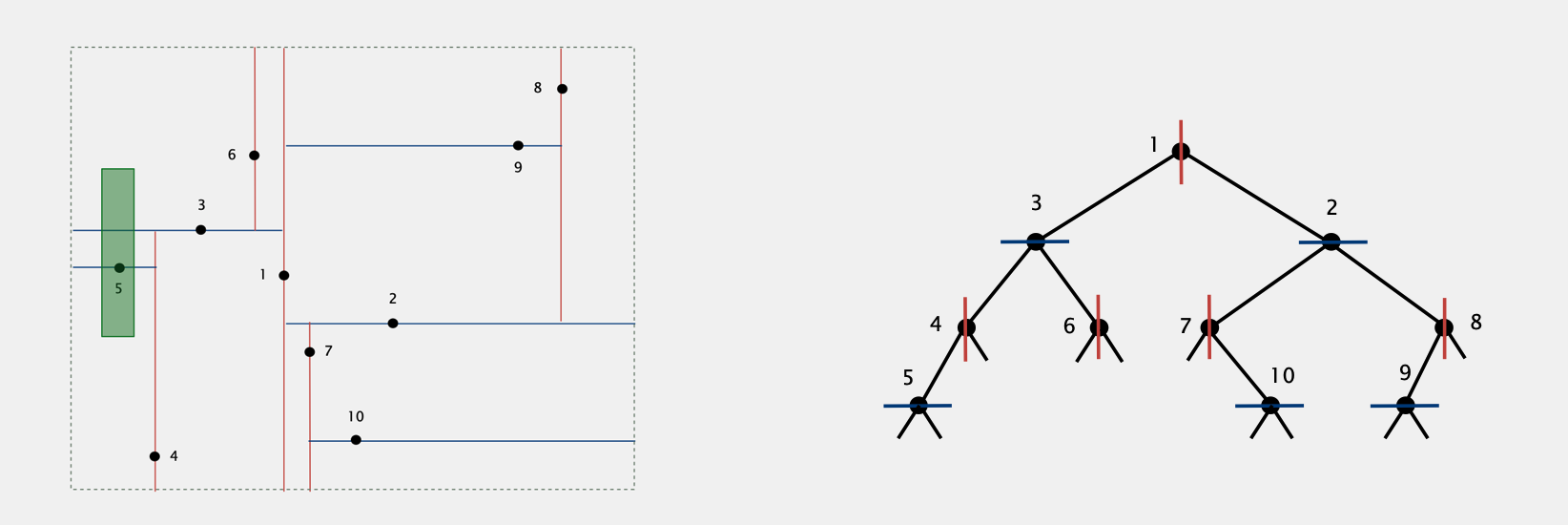
2-DTree.png
2-DTree.png

  1. 每个点表示为一个key，包含一个二维坐标。

  2. 我们将数据点依次插入到一个二叉搜索树中：

    1. 对于树中奇数层的点，其左子树的点为平面中在该点左边的点，其右子树中点为平面中在该点右边的点 （e.g. 以点1为例，左子树中3，4，5，6都在点1的左边，2，7，8，9，10都在点1的右边，相当于以点1为基准将平面分为左右两部分）

    2. 对于树中偶数层的点，其左子树的点为平面中在该点下边的点，其右子树中点为平面中在该点上边的点 （e.g. 以点3为例，左子树中4，5都在点1的左边，6在点1的右边，相当于以点3为基准将子平面分为上下两部分）

      这样我们每插入一个点，就将一个平面分为两个更小的平面

Range Search in 2-D Tree

e.g. 假设我们需要搜索上图中绿色框范围内的点

  1. 从根节点开始，判断节点是否在范围内，如果在则添加到结果集
  2. 对于在奇数层的节点，如果查询范围的左边界在该节点左边，则递归查找到左子树，如果查询范围的右边界在该节点右边，则递归查找到右子树
  3. 对于在偶数层的节点，如果查询范围的上边界在该节点下边，则递归查找到左子树，如果查询范围的下边界在该节点上边，则递归查找到右子树
  4. Complexity：R + logN

2-D树的补充应用：Find Nearest Neighbor

给出一个点，找出现存平面中离该点最近的点

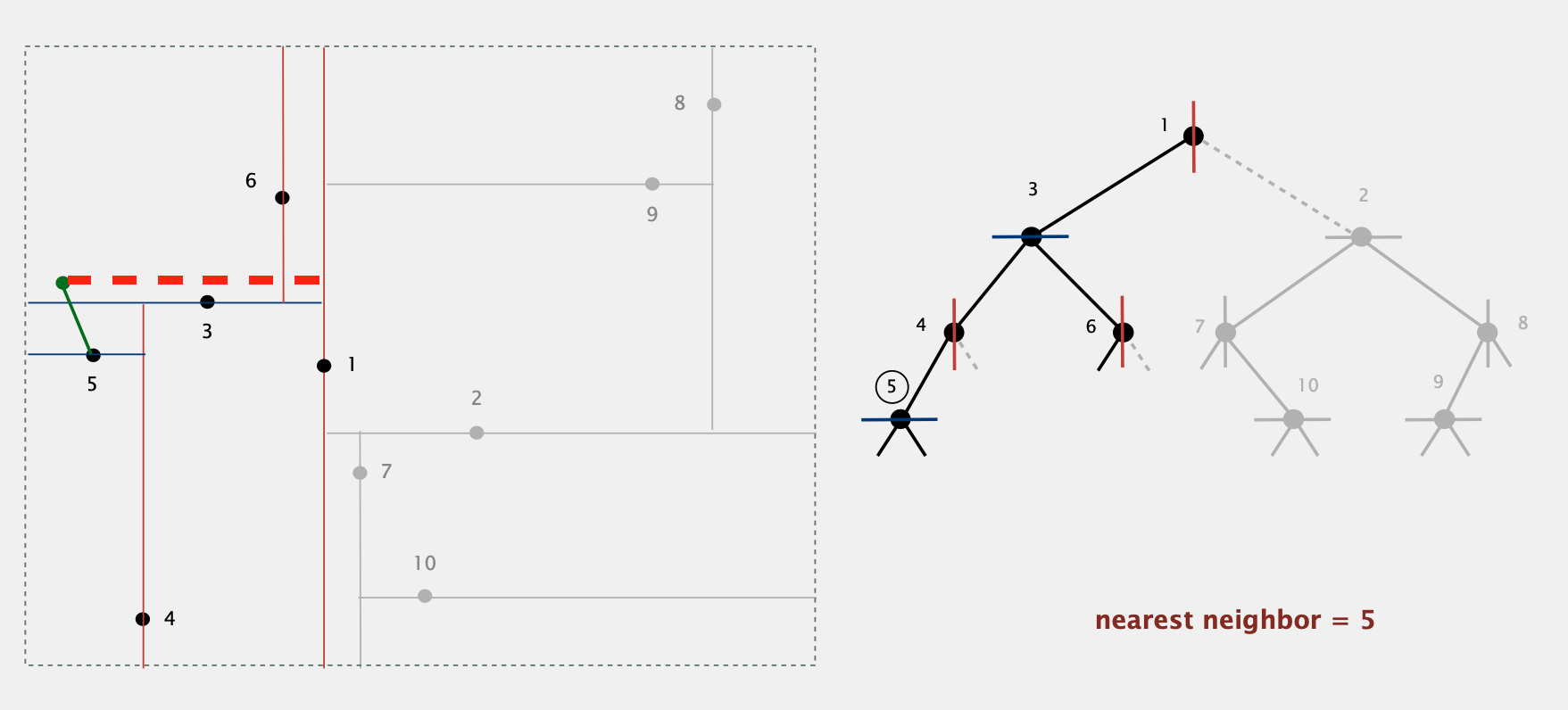
KDNearestNeighbor.png
KDNearestNeighbor.png
  1. 从根节点开始，计算该节点与目标节点的距离，并更新最短距离
  2. 目标节点应该在该节点划分的两个区域的任意一边，我们优先递归到包含目标节点的区域对应的子树（e.g. 图中目标节点在1节点的左边，因此我们先递归到左子树，即3节点）
  3. 递归完包含目标节点的一边后，我们再判断是否需要递归另外一边的子树（e.g. 递归完1节点左半部分后，得到最近的neighbor为节点5，此时当前最短距离小于1节点右边的理论最短距离（即红色虚线的长度），因此1节点右边的节点与目标节点的距离不可能小于当前的最短距离，因此我们不需要再递归右节点部分，相当于剪枝）
  4. Complexity：logN（in average），N（worst case, even if tree is balanced）
KD Tree
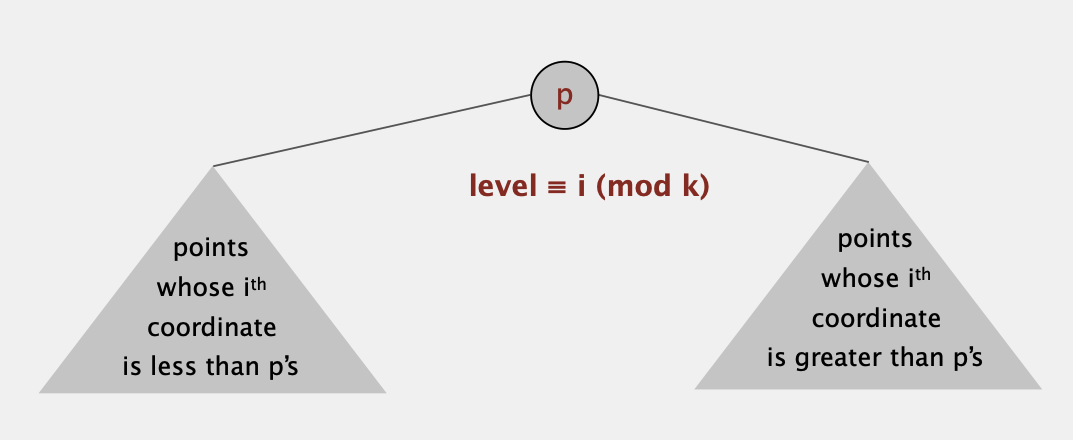
KDTree.png

类似于2D-Tree，奇数层的节点将平面分为左右两部分而偶数层的节点将平面分为上下两部分，我们同样利用BST将其延伸到k维。

假设节点P在第i mod k 层，则P的左子树的点在第i维都比点p小，右子树的点在第i维都比p大

Interval Search Tree

1D Interval Search Problem

我们希望实现一种数据结构，能够保存一系列区间（interval），这些区间有可能存在重叠（overlap）

这个数据结构能够完成如下操作：

  1. insert：插入一个interval (lo, hi)
  2. search：搜索一个interval (lo, hi)
  3. delete：删除一个interval (lo, hi)
  4. interval intersection query：给定一个interval (lo, hi)，找出所有和这个interval交错（intersect）的区间

（我们假设所有interval的起点都不同）

Implementation

利用BST，每个节点存储一个interval，但只用interval的左端点（即lo值）作为BST每个节点的key。

另外每个node还要存储以该node为根节点的树中所有节点最大的右端点，记为max （图中蓝色部分）

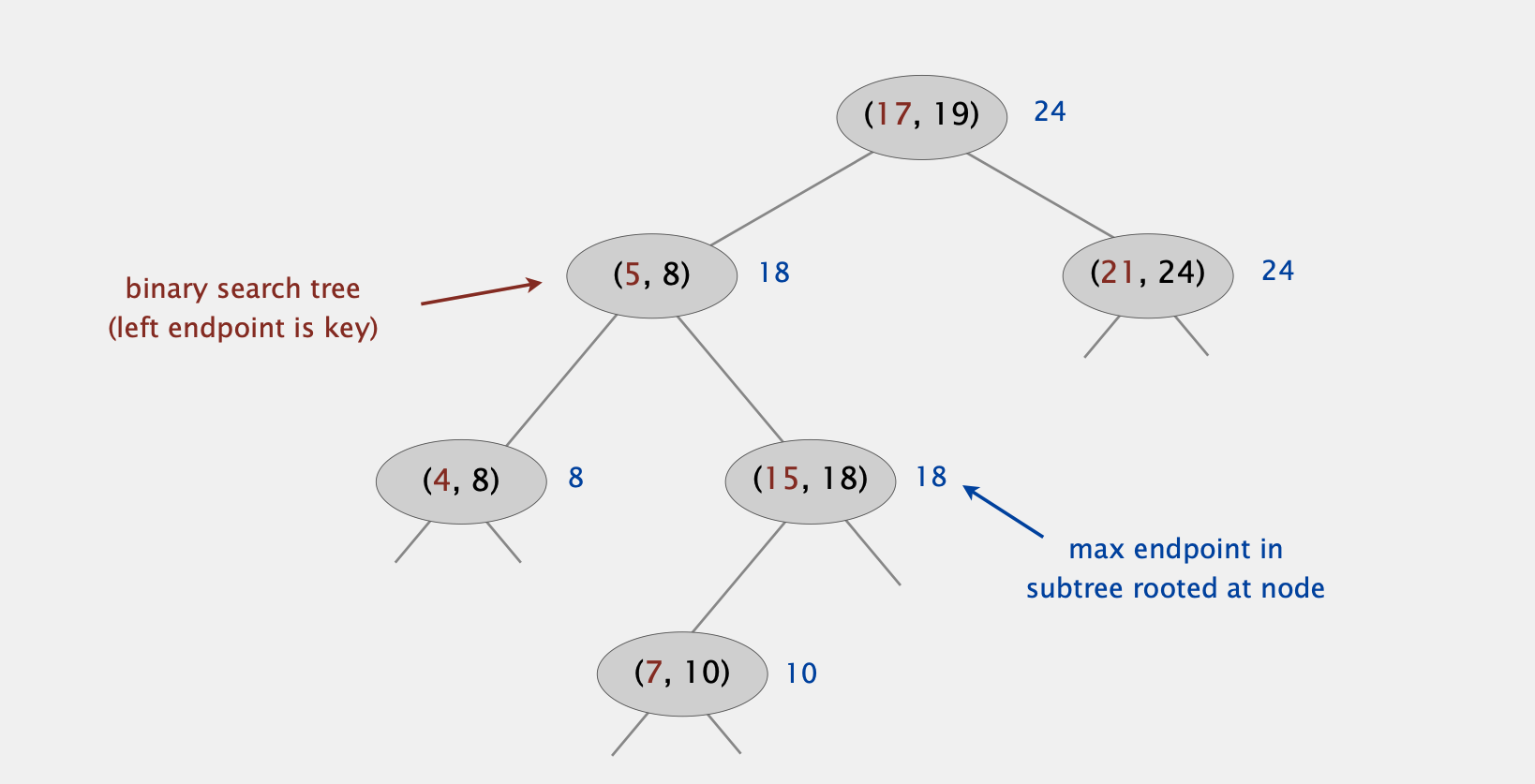
IntervalST.png

Insertion

插入操作等同于一般BST的插入，以interval的左端点为key查找到对应的插入位置。

插入到对应位置后，要延搜索路径回溯并更新路径节点上的max值

Interval Intersection Search

假设给出一个query interval (lo, hi)，只需要查找到一个与其交错的interval

从根节点开始，对每个节点表示的interval

  1. if 该interval和query interval交错，则将其添加到结果集
  2. else if 该节点的左子树为空，递归到右子树
  3. else if 左节点的max值小于query interval的lo值，递归到右子树 （即所有左子树中的节点都在query interval的左边，不可能存在交叉）
  4. else 递归到左子树
1
2
3
4
5
6
7
8
Node x = root;
while (x != null) {
	if (x.interval.intersects(lo, hi)) return x.interval;
	else if (x.left == null) x = x.right;
	else if (x.left.max < lo) x = x.right;
	else x = x.left;
}
return null;

有效性证明：

  1. 当我们搜索右节点时，代表左子树中不可能存在任何交错的节点区间

  2. 如果我们搜索左节点，如果在左子树中找不到交错的区间，代表即使我们搜索右子树也不可能找到交错的区间节点

    证明：假设左子树不存在交错节点，同时因为搜索左子树，代表左节点的max值大于或等于query interval的lo值（即左子树中存在右端点大于lo的区间）。

    因此如果在左子树中找不到交错节点，代表左子树中所有区间的最左端点都在query interval的右边（即图中hi < c）。又因为右子树中所有区间的左端点肯定大于左子树的最左端点，因此右子树中也不可能找到交错节点

延伸：如何找出所有与其交错的intervals

按上面找一个intersection的方法，每找到一个交错interval，将其删除（或标记为已找到并不再访问），直到找到所有的interval

Complexity：我们可以采用红黑树，使得对insert, delete, search和find one intersect interval操作的复杂度为logN，对find all intersect interval，假设最后结果集的大小为R，则复杂度为RlogN（即需要R次find one intersect interval操作）

Application：Orthogonal rectangle intersection

平面内有一系列长方形（有可能存在相互覆盖或交错），找出所有交错的长方形

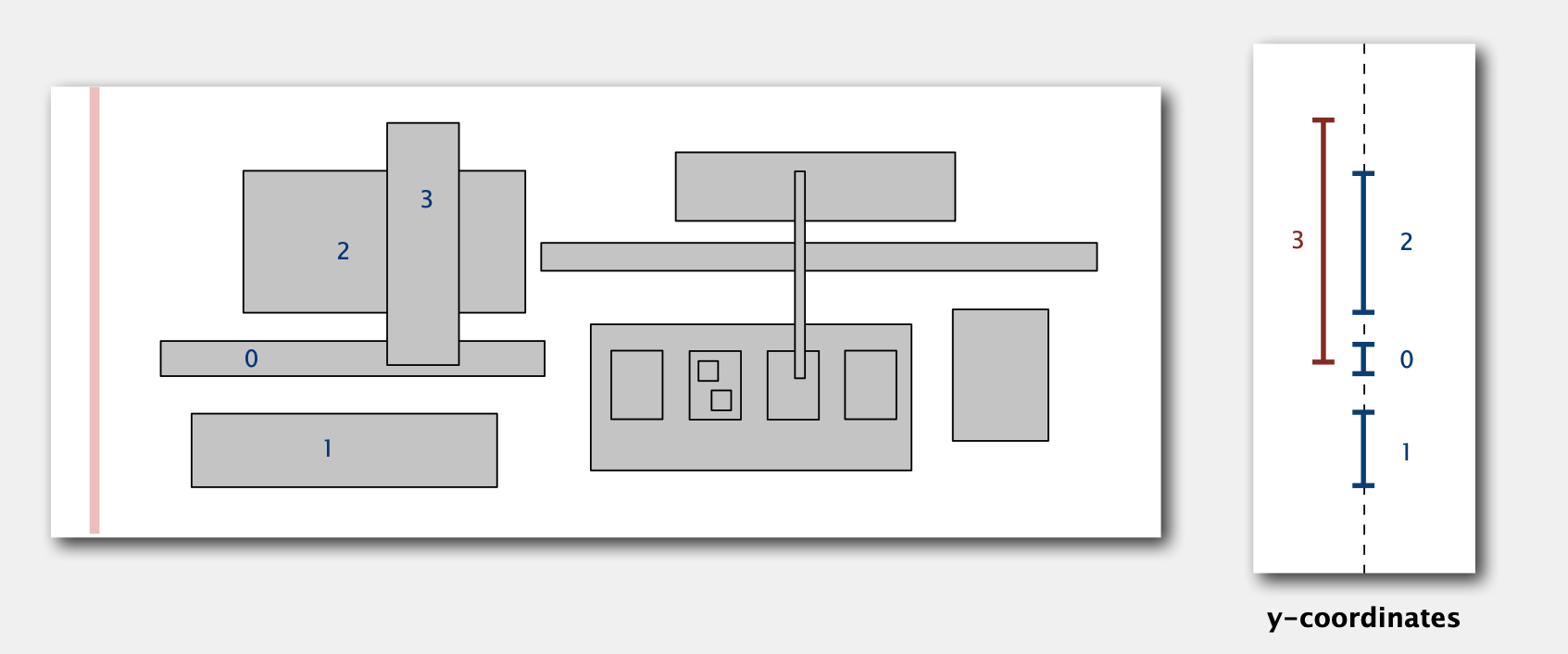
RectIntersectSearch.png
RectIntersectSearch.png

算法：Sweep Line Algorithm 线性扫描法（类似于1-D range search）

从左到右扫描所有长方形，每个长方形有一个y-interval记录长方形的上下两边的y值区间。我们用一个Interval Search Tree存储长方形的y-interval

  1. 扫描到一个长方形左边时：
    1. 查找Interval Search Tree中与该长方形y-interval交错的长方形，并记录到结果集
    2. 将这个长方形的y-interval插入到Interval Search Tree中
  2. 扫描到一个长方形右边时：将这个长方形的y-interval从Interval Search Tree中移出

复杂度：NlogN + RlogN

  1. 将所有长方形按x值排序以便扫描（NlogN）
  2. 所有长方形的y-interval插入到Interval Search Tree中（NlogN）
  3. 删除Interval Search Tree中的y-interval（NlogN）
  4. 搜索交错的区间（NlogN + RlogN）

该问题为原本2D Orthogonal line segment intersection的升级版，即2D orthogonal rectangle intersection。该算法将原本问题降维至1D interval search，因而降低了时间复杂度

BST几何应用总结
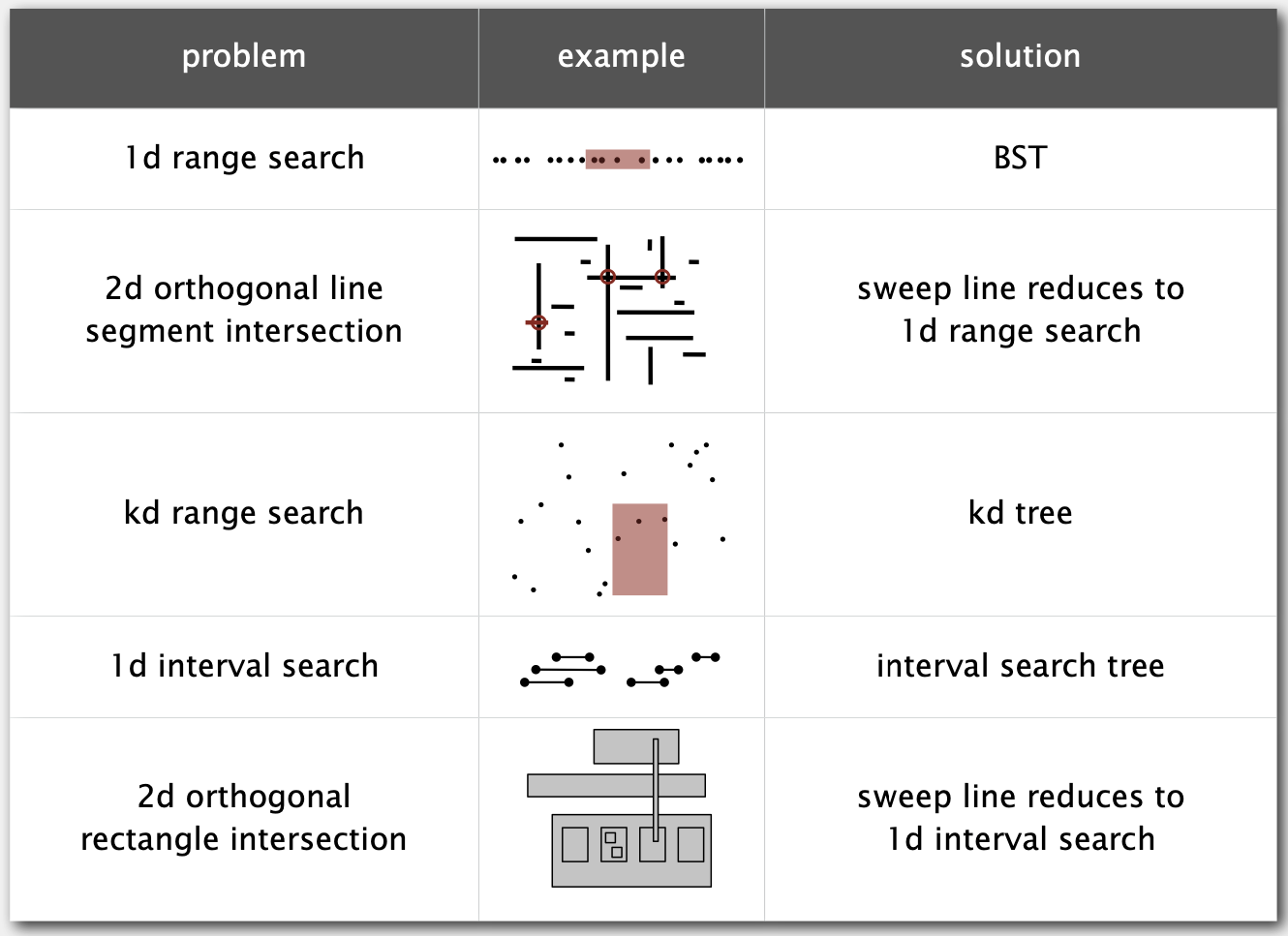
BSTGeometricAppConclusion.png
BSTGeometricAppConclusion.png

Week 6. HashTable 哈希表

哈希表本质是一个Space-Time Trade-Off的数据结构，相比其他Symbol Table实现（如BST，红黑树），插入和查找的速度更快，但不支持ordered operations

我们将key-value键值对存储在一个数组中，并实现一个hash function以获得某个key在数组中的index

为此我们需要解决以下问题：

  1. 如何设计hash function
  2. 如何判断两个key是否相等（Equality Test）
  3. 如何解决两个不同的key具有相同的hash值（Collision Resolution）

Hash Function 哈希函数

我们希望Hash Function计算效率要高，且每个计算出的index出现的可能性尽可能相等（e.g. 假设key1-10十个数，key1-9的hash都为0而key10的hash为1，这样会造成大量的hash冲突）

hashCode()

对于一个任意类型的对象，我们使用hashCode()函数将其简化为一串数字（介于Integer.MIN_VALUE和Integer.MAX_VALUE之间），便于之后我们设计的hash函数通用化。hashCode()函数需要满足以下要求：

  1. 两个相等对象的hashCode相同，即当x.equals(y) == true时, x.hashCode() == y.hashCode()

  2. 尽可能满足（不一定）当两个对象不同时，其hashCode也不同。即x.equals(y) == false时x.hashCode() != y.hashCode()。

    因此hashCode()函数如果只返回一个常数(e.g. 17)是满足要求的，但没有什么实际用途。

标准方法（Horner’s method）：31x+y

我们先设置一个初始hash值为17（一个质数），然后对于自定义数据结构中的每一个field，我们都采用hash = 31 * hash + field.hashCode()来计算：

  1. 如果field为原始数据类型，则将其转化为包装类型（wrapper type）再使用其hashCode()函数
  2. 如果field为包装类型或引用类型，则直接采用其hashCode()函数
  3. 如果field是一个数组，则对其中的每一项采用hashCode()函数和31x+y规则（或者直接使用Arrays.deepHashCode()函数）。

补充：所有java的class都内置了hashCode()函数。默认情况下，hashCode()为对象的地址。包装数据类型有其设计好的hashCode()函数

hash()

假设我们可以使用的数组空间大小为M，则我们的hash()函数为：

1
2
private int hash(Key key)
{ return (key.hashCode() & 0x7fffffff) % M; } // 注意

注意：因为key可能存在负数，因此我们需要先转成正数后才能进行取模操作。

另外我们不能直接用Math.abs()取正数，因为当hashcode为Integer.MIN_VALUE时该操作会导致整数溢出

Uniform Hashing Assumption

假设数组空间大小为M，且每个key获得0~M-1的index的概率都是相同的

从概率论角度，当我们随机插入~ sqrt(πM / 2)个key后，会出现两个key有相同的index

当随机插入~ MlnM个key后，数组每项都会存在至少一个key

当随机插入M个key后，数组中包含最多key的项大概包含log M / log log M个key

Collision Resolution 冲突解决

即使我们采用了均匀分布的hash函数，仍然可能存在不同的key具有相同的hash值，即hash冲突

Separate Chaining 链表法

假设我们的index数组大小为M < N（待插入的键值对数量）。我们对数组中每一项放入一个链表，对于相同hash值的key所对应的键值对将插入到对应的同一个链表。

  1. Hash：先用hash函数计算key在表中的index i （0 <= i <= M-1）
  2. Search: 找出数组中的第i项，对其链表进行线性查找
  3. Insert：如果key不存在则将键值对插入到对应的链表头部。如果存在则改变对应的value值

平均情况下，每个链表的长度为N/M，因此Search和Insert的复杂度也为~N/M

M的选择不能过大和过小，一般我们希望平均链表长度为5，此时M ~ N/5，复杂度趋近于log 1

Opening Addressing 开放地址法

又称为linear probing线性探测法

Insert：仍然使用hash()函数获取key-value在表中的index，当这个index在数组中已被占用时，从这个index开始向后遍历（index + 1, index + 2, …），直到找到一个空的index将键值对插入

（注意这里index遍历是循环的，即当index遍历到数组最后一位后，回到数组开头）

Search：获得index后查找对应位置是否存在key，如果key不相同则继续向后遍历，直到遇到空位置

注意：index数组的大小M >= N，以保证所有数据都能够被插入

Complexity

当数组是半满的情况，每次插入或查找需要的平均探测次数（即依次遍历找到空位的次数）为~3/2

当数组是接近全满后，每次插入或查找的平均探测次数为~ sqrt(πM / 8)

即数组越满，插入和查找的效率越低

HashTable 和 Balanced BST对比

HashTable Balanced BST （R-B BST）
代码更为简单 性能更稳定
对于较为简单的key而言效率更高 支持Ordered Operations
HashMap TreeMap，TreeSet

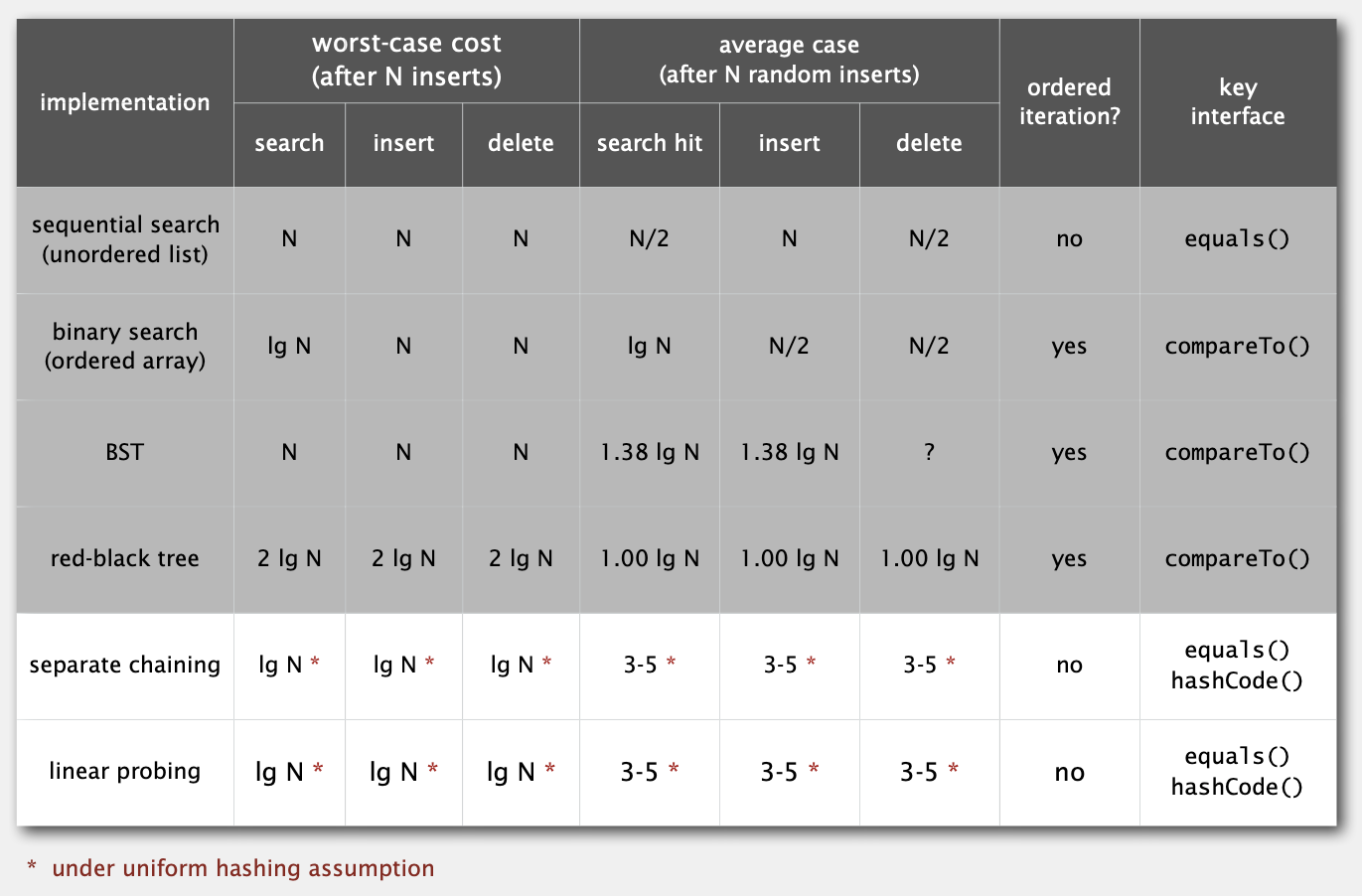
几种ST实现比较

STcomparasion.png
STcomparasion.png